AIC 2
This is part 2 of my article on AIC. Originally it was part of the original
article but it got so long that I felt it was detracting from the focus of
the original, so I decided to split the article into 2. Please read part 1
if you're unfamiliar with the concept of AIC.
With the knowledge from part 1 you can solve roughly 99.8% of randomly
generated Sudoku puzzles. Everything within this subsequent article builds
on that basic introduction in order to raise that number as close to 100% as
possible. The skill ceiling for Sudoku is extremely high and there are many puzzles
that cannot be solved with classical AIC. To climb the ladder of difficulty
we will have to define more types of strong inferences.
Table of Contents
Grouping Premises
Until now we've only been considering inferences between a single pair of
candidate premises. However if you can prove that a whole set of premises
cannot all be false at once then they form what's known as a
strong inference set, and any division of this set into two subsets
(groups) will give you a strong inference between the subsets. These subsets
can be overlapping, the only restriction is that every element of the
original set has to be in at least one subset.
All instances of a digit in a row, column or box form a strong inference
set. Additionally, all the candidates within a cell form a strong inference
set, but this case is not as easy to make use of.
For a practical demonstration, in the example below, the 9s in column 8
form a strong inference set because at least one of them must be true (every
column needs a 9). We can split this into two premises: 9 being in r8c5 and
9 being contained within box 9.
The most practical way to group premises is by mutual weak inferences, as
it allows you to continue the chain.

(8)r1c8 = r1c7 - (8=9)r7c7 - r89c8 = (9)r5c8 =>
r5c8<>8
All the instances of 9 in column 8 form a strong inference set. Notice that
these 9s are contained within 2 boxes, so we can group them into two subsets
depending on which box they're in. This gives us a strong inference between
the two subsets: {9r5c8} = {9r8c8, 9r9c8}.

Three Grouped strong inferences obtained by grouping the candidates in a
row according to the box they're contained in

(1)r4c1 = r4c8 - c8b3 = (1)r1b3 => r1c1<>1
The strong inference set here is comprised of all the 1s within box 3. 1
can be in r1c7, r1c8, r1c9, r2c8 or r3c8. All these cells are contained
within either row 1 (blue), or column 8 (purple), or both (pink) - so I've
grouped them into these two subsets. The grouped link formed by this is
referred to as an Empty Rectangle Intersection (ERI) because
the other cells in that box form a rectangle. Blame whoever
named this move years ago if you find that confusing.
The first group contains the candidate premises 1r1c7, 1r1c8 and 1r1c9. The
second group contains 1r1c8, 1r2c8 and 1r3c8. The fact that 1r1c8 is
contained within both groups means this is an example of a strong inference
where the premises involved do not also have a weak inference - both can be
true if 1r1c8 is true.
Alternatively, you can split these into two groups with no overlap and
still successfully obtain the elimination:
{1r1c7, 1r1c9} = {1r1c8, 1r2c8, 1r3c8}
{1r1c7, 1r1c8, 1r1c9} = {1r2c8, 1r3c8}
But it is simpler to define the Empty Rectangle as the intersection between
a row and a column within a box, hence (1)c8b3 = (1)r1b3.
Adding these Grouped strong inferences to your repertoire will allow you to
solve maybe 50% of the "Beyond Hell" difficulty puzzles on sudoku.coach. But
to solve more than that, we're going to need even more complex strong
inferences.
Almost Locked Sets
An Almost Locked Set (ALS) is a set of N cells within a region that
together contain N+1 unique digits.

(1478)r9c578: 3 cells containing 4 digits
If any of these digits were removed from the ALS you would have a locked
Triple containing the remaining 3 digits. We can use this relationship to
prove new strong inferences. The typical way to do this is to simply say
there's a strong inference between the extra digit and the resulting locked
set. This gives us four strong inferences:
(1=478)r9c578
(4=178)r9c578
(7=148)r9c578
(8=147)r9c578
The locked set's weak inferences are just its potential eliminations, which
is every candidate in a cell that sees every instance of that digit within
the ALS.

(7=184)r9c578 - r8c8 = (4)r8c4 => r8c4<>7
This AIC proves a strong inference between (7)r9c5 and (4)r8c4, so we can
eliminate any mutual peers. It is standard to push the digit that continues
the chain to the end of the LS in Eureka notation to make the continuity of
the chain more apparent, hence (7=184)r9c578.
Only two of the ALS digits are relevant to the chain as a whole - the 4s
and 7s - so I often ignore the rest and treat ALS strong inferences as being
between the two groups of digits, effectively (7)r9c5 = (4)r9c78. Any two
ALS digit sets cannot be false at the same time because then the N cells
would have N-1 unique candidates, meaning it would be impossible to fill
them all. This has the effect that every digit in the ALS is strongly linked
to every other digit.

The same AIC with the strong inference directly between the ALS digits
(4=7).
It's not a big deal which of these you use when chaining, they're both
valid and lead to the same result in the end, so it's up to whichever you
find most convenient.

(1)r1c2 = r1c5 - (1=87)r7c56 - (7=3681)r4567c2- => r28c5<>1,
r7c78<>8, r8c56<>8, r2c2<>1, r12c2<>8,
r6c1<>8
Another important thing to note about ALS is how they act in Rings. Focus
on (178)r7c56.
Recall that when an AIC forms a Ring, all of its weak inferences are proven
to also be strong. By the same token, all strong inferences are also proven
to be weak. This has profound consequences for ALS: if two of the candidate
digits have a weak inference, that means both of them cannot be true at
once. Rephrased, this means exactly one of the candidate digits used in the
Ring (1 and 7) must be false.
As an ALS is composed of N+1 candidate digits in N cells, exactly one of
those candidate digits is false. The Ring just proved that either 1 or 7
must be false, therefore the other candidate digits in the
ALS must be true. In this case the other candidate digit is 8, so we can
eliminate all the 8s that it sees.
Same goes for the other ALS, (13678)r4567c2. The AIC proves a weak inference between (1) and (7), so all the
other digits are locked into the ALS: the ALS must contain 3, 6 and 8.
Almost Hidden Sets
An Almost Hidden Set (AHS) is a set of N digits within a region that are together contained within N+1
unique cells. It can be seen as complimentary to ALS - every ALS has an
equivalent AHS and vice versa.

(56)r9c124: 2 digits contained within 3 cells
If the (56) candidates were removed from one of the AHS's cells, the
remaining cells would become a hidden set. Again we can use this to define
new strong inferences. The Eureka notation for AHS isn't standardised as far
as I know, so I'd like to take the opportunity to advance my own standard
for them. This AHS gives us three strong inferences:
(56)(r9c1 = r9c24)
(56)(r9c2 = r9c14)
(56)(r9c4 = r9c12)
The strong inference is between the premises that (56) is contained within
particular cells in row 9. The weak inferences of an AHS are a bit more
complicated than for ALS: there are cellwise weak inferences for every cell
of the AHS (r9c124), and also regional weak inferences from every cell that
contains only one AHS digit. If this cell was part of the hidden set, it
would have an exposed naked single, so it would eliminate all other
instances of that digit in its row/col/box.

(8=7)r8c5 - r8c2 = r9c2 - (56)(r9c2 = r9c14) =>
r9c4<>8
This AIC proves that at least one of the endpoints (8)r8c5 and (56)(r9c14)
must be true. The AHS weak inference here is cellwise within r9c2.

(9=3)r6c1 - (39)(r5c2 = r5c75) - (1)r5c5 = (1)r6c4 =>
r6c4<>9
This AIC shows off the regional weak inferences from an AHS cell containing
only a single candidate, 3. I extend the convention from ALS to AHS by
putting the cell that continues the chain at the end of the AHS strong
inference (39)(r5c2 = r5c75).

(1)r1c2 = r1c5 - (1=87)r7c56 - (74)(r7c2 = r21c2)- => r28c5<>1,
r7c78<>8, r8c56<>8, r2c2<>18, r1c2<>8
As this is a Ring all the weak inferences are also strong inferences and
vice versa - the strong inferences are all weak inferences.
This has important ramifications for an AHS: we just proved that in the
pink AHS the strong inference between (47)r7c2 and (47)r1c2 is also weak,
so both cannot be true at the same time - recall that an AHS is formed
from N digits being present within N+1 cells.
If we know that two of the cells cannot both contain AHS digits, that
means one of these two cells must not contain the
AHS digits, which further implies the other AHS cells must contain
the AHS digits, therefore we can eliminate every other candidate from
them. In this example, 1 and 8 are removed as candidates for r2c2.
- - -
You won't see AHS often on Sudoku websites. There are two main reasons for
this: the first is that they're quite hard to spot when you scan the grid,
they are "hidden" after all. I miss hidden pairs all the time when I'm
solving puzzles.
The second reason is that most of the time there's an equivalent ALS that
can achieve the same thing. Here are the first two examples from this
section with their AHS replaced by the equivalent ALS:
(8=7)r8c5 - r8c2 = r9c2 - (7=148)r9c578 => r9c4<>8
(9=3)r6c1 - (3=41)r5c28 - r5c5 = (1)r6c4 => r6c4<>9
So the major use-case for them is to simplify a chain by replacing for
example a 7-cell ALS with a 2-digit AHS. However, there is a rare case where
two AHS can intersect in such a way that there is no equivalent ALS. I wrote
about it further in another article so I'll only show one example.

(514)(r4c9 = r4c342) - (2695)(r4c2 = r1589c2) =>
r9c9<>5
This is an AIC formed by two intersecting AHS. The weak inference (14)r4c2 - (29)r4c2 is easy to prove as all the candidates are
contained within the same cell, so both AHS cannot contain that
cell.
There is no equivalent AIC that you can obtain by replacing these AHS by
their ALS counterparts, as their counterparts are actually two intersecting
AALS (N+2 candidates in N cells).
Kraken Fish
If a candidate digit's locations in N base regions are contained within N
intersecting regions then you can eliminate that candidate from all non-base
positions in the intersecting regions. This is called a Fish and the common
cases are the X-Wing, Swordfish and Jellyfish for N = 2, 3 and 4
respectively.
If however these candidates are contained within N+1 intersecting regions,
this is 1 candidate or set of candidates off of being a Fish, so it's called
"Almost Fish" or "Kraken Fish". This gives us a strong inference between the
Fish and the extra candidates, which are known as the "Fins". The most
common example of this is a Finned X-Wing.

(1)r5c1 = (1)r58/c35 => r46c3<>1
Fishing is a very complicated subject so please refer to the Ultimate Fish Guide for all there is to know on the matter. For the sake of this section
it is necessary to establish some basics.
- Fish are defined by their base sets and their cover sets. If all the candidates of N base sets can be covered by N cover sets, all non-base candidates can be eliminated from the covers.
- If however you require N+1 cover sets to cover all the candidates, you can only eliminate candidates that are contained within 2 cover sets.
- Furthermore, if you require N+X cover sets, you can only eliminate candidates that are contained within X+1 cover sets. The value X is known as the "Rank".
When putting Fish into Eureka notation, you list the base sets first, then
a slash (/), then the cover sets. This Kraken Fish is thusly expressed as
(1)r58/c35.
The Finned X-Wing can be expressed as an N+1 type Fish: (1)r58/c35b4. Box 4
is the extra cover set required to cover all candidates in rows 5 & 8,
and the candidates that are contained within 2 cover sets can be eliminated.
These are the candidates contained within the intersection of c3 and b4. If
the Fish can be resolved into an elimination like this it's not typical to
call it a Kraken Fish, it's just a Finned Fish. "Kraken Fish" implies some
AIC chaining through other digits.
If you find an N+1 type Fish with no candidates contained within
overlapping cover sets then all hope is not lost: you can call the extra
Fins that require the +1 cover set the "Kraken candidates" and define a new
strong inference "Kraken candidates = Fish". This is a whole load of
complicated terminology so another example is in order.

(8)c24/r69 = (8-6)r7c2 = r8c1 - (6=8)r3c1 => r6c1<>8
This AIC proves that the endpoints (8)c24/r69 and (8)r3c1 have a strong
inference so at least one must be true. Both cases would eliminate 8 from
r6c1 so we can safely eliminate it.
The Kraken Fish strong inference is a type of Grouped link: there has to be
an 8 in column 2 so the 8s form a strong inference set. If we divide them
into the two subsets {8r7c2} = {8r6c2, 8r9c2} we have a new strong
inference. The second subset stands for the premise that 8 is only contained
within r69c2, and if this is true then the Fish is true. Again the Fish's
weak inferences (not showcased here) are just its potential eliminations
because the fact the Fish eliminates them means they cannot co-exist - both
cannot be true.
Avoidable Pattern Guardians
An Avoidable Pattern is an arrangement of candidates that provably cannot
be part of the solution. There are two major types of Avoidable
Patterns:
Impossible patterns are candidate arrangements that are simply
impossible to solve, any attempt to fill in the cells according to the
candidates will result in you being unable to do so according to the rules
of Sudoku. This is quite a broad definition with a lot of potential for
interpretation but there are many well-defined impossible patterns which can
be easily recognised. Examples include Bivalue & Trivalue Oddagons and
negative-rank patterns
such as Broken Wing (a single-digit Oddagon).

Deadly patterns are candidate arrangements that can only have
multiple solutions. If they are included within a greater candidate field
then this candidate field either has 0 or multiple solutions. If you know
the puzzle you're solving has a unique solution, removing candidates can
never produce more valid solutions, so if you encounter a deadly pattern
you've made a mistake and ended up in an unsolvable state with 0 solutions.
Examples include
Unique Rectangles and the BUG state.
You absolutely do not want to see an Avoidable Pattern in your puzzle so
you do not want to eliminate the extra candidates that are preventing one
from appearing. The candidates preventing the impossible state are called
the Guardians.
If there is only one of these candidates you can place it as a solved cell,
but if there are more you can treat them as a strong inference set and use
them in AIC - you know that at least one of them must be true.

(2=6)r5c6 - (6=2)r2c28- => r2c1<>2, r2c7<>26
The blue cells would form a Bivalue Oddagon if they all contained {45} so
the extra candidates are the Guardians. They form a strong inference set
which I've grouped by their digits. The resulting strong inference combines
with the bivalue cell (26)r2c6 to form a Ring which is effectively a naked
Pair.

(8)r2c46 = r4c46 - (8=4)r5c5 - r5c4 = (4)r1c4 =>
r1c4<>8
The blue cells here would form a Unique Rectangle if they all contained
{23} so the extra candidates are the Guardians. They form a strong inference set
which I've grouped by their boxes. A short AIC proves a strong inference
between (4)r1c4 and (8)r2c46 leading to one elimination.
Fireworks
Fireworks are a wonderful and surprisingly recent idea, being advanced only
three years ago by shye. The basic gist is that "when a candidate in an intersecting row and
column is limited to the same box, it must be placed in the intersecting
cell".

Take this arrangement of candidates for example. If (1)r1c9 and (1)r9c1 are
both set to false then box 1 would have two separate instances of claiming
candidates, resulting in 1 being placed in r1c1.
It follows that these blue cells form a strong inference set: all of them
cannot be false at once. If they were, you would be forced to place two 1s
in box 1 which is impossible.
In my experience if the Fireworks are only present on a single digit they
have limited utility and most if not all AIC constructed with these links
can be expressed via Kraken Fish instead. Still, the simplicity & added
power when there are two or more overlapping sets of Fireworks (check the
original thread linked above, and
this thread) make it
worth learning.
Equivalence
"Equivalence" is a placeholder name for a particular logical relation
outside of strong & weak inferences. If two premises are always true at
the same time and always false at the same time, these premises are said to
be equivalent, and any resulting structures such as Fish or Locked Sets are
also equivalent.
If you have the strong inference A = B, but you also know B is equivalent
to C - when B is true C is true, when B is false C is false, and vice versa
- then you can swap it out for the new strong inference A = C and all chains
resulting from this are still valid. I tentatively propose that this should
be notated as A = B + C.
These equivalences can be proven under certain circumstances between the
three major logical structures in Sudoku: ALS, AHS and Fish. The three
possible pairs are ALS+AHS, ALS+Fish, and AHS+Fish.

AHS+ALS
In this puzzle row 5 has an AHS (12)r5c258, marked in blue. This gives us
strong inferences between the premises that each of these cells contains the
AHS digits (12).
(12)r5c2 = (12)r5c5
(12)r5c2 = (12)r5c8
(12)r5c5 = (12)r5c8
Note that when the premise (12)r5c2 is true, it clears all other candidates
from the cell r5c2 and the new contents of the cell combine with r2c2 to
form a Locked Pair, marked in purple. When (12)r5c2 is false this Locked
Pair is invalid as the two cells contain too many digits. So the premise
(12)r5c2 can be considered equivalent to the premise that the Locked Pair is
valid, as they always come together. We can represent this as (12)(r5c5 =
r5c82) + (12)r25c2, or the reverse, (12)r25c2 + (12)(r5c2 = r5c58).

(38)(r5c6 = r5c31) + (38)r25c1 - (3)r3c1 = (3)r3c56 =>
r12c6<>3
This puzzle has a similar setup. The premise (3)r5c6 has a strong inference
with (38)r5c1 thanks to the AHS, and this latter premise is equivalent to
the Locked Pair (38)r25c1, so the chain continues from its weak
inferences.
I'm afraid that aside from serving as an introduction to the equivalence
concept, these ALS+AHS combinations are limited in their practicality as (as
far as I know) every instance can also be considered a case of the cellwise
double AHS intersection. Replace the above (38+)r25c1 ALS with its dual AHS
(259)c1, and you get this AIC:
(38)(r5c6 = r5c31) - (259)(r5c1 = r673c1) - (3)r3c1 = (3)r3c56
So the major use-case would be to simplify a complicated chain by replacing
a (for example) 7-cell AHS with its 2-cell ALS counterpart. Disappointing
but I promise the ALS+Fish equivalence is a lot more exciting.

ALS+Fish
In this puzzle row 5 has an ALS (123)r5c28, marked in blue. This gives us
strong inferences between the premises that the ALS contains each of its
candidate digit sets.
(1)r5c28 = (2)r5c28
(1)r5c28 = (3)r5c28
(2)r5c28 = (3)r5c28
Note that when the premise (1)r5c28 is true, it clears all other 1s from the region it is contained
within (row 5), so when this premise is true row 5's possible positions
for 1s are reduced to the strong inference set (1)r5c28. This strong
inference set can be used as a base set for the X-Wing (1)r58/c28. So when
the premise (1)r5c28 is true the X-Wing is valid, but when (1)r5c28 is
false the X-Wing is invalid because the column cover sets no longer cover
every candidate within row 5. The premises (1)r5c28 and (1)r58/c28 are
thus equivalent and can be freely replaced in any AIC.

(9)r123c2 = r6c2 - (9=18)r6c19 + r68/c19 - (8=9)r3c1- =>
r6c25<>1, r6c56<>9, r7c1<>8, r4c9<>8
In this puzzle the premise that the ALS (189)r6c19 contains 8 is equivalent
to the premise that the X-Wing (8)r68/c19 is valid so they can be freely
swapped out. This gives us a Ring with plentiful eliminations.
In Xsudo language this AIC is composed of 5 truths: 9c2, 8r8, r3c1, r6c1,
r6c9. The candidates are covered by the 5 cover sets 1r6, 9r6, 8c1, 8c9,
9b1. 5 - 5 = 0 so the move is rank0.
In fact the entire puzzle is solvable using moves consisting of 5 or fewer
truths, putting it at the lower end of difficulty in this metric - despite
this, its SE rating is 9.0, and it requires Whips and Braids of length 7 to
solve. YZF's solver can't find a single rank0 move - no Rings, ALS-Rings,
Blossom Loops, MSLS, nothing. All this hints that the ALS+Fish equivalence
has a powerful nature inherent to it which makes its eliminations very
difficult to obtain with standard AIC & FC procedures.

(6=57)r2c39 + r27/c39b9 - (7=4)r9c9 - (4=6)r9c4 - r4c4 = (6)r4c1 =>
r12c1<>6, r5c3<>6
Another example except in this case the equivalent X-Wing is Finned so its
only potential eliminations (weak inferences) are (7)r8c9 and
(7)r9c9.
There is also the AHS+Fish equivalence but it's quite redundant as ALS are
easier to use. I won't go into detail but it works the same way by
effectively giving the AHS premises more weak inferences.
Almost-AIC
You may have noticed a pattern in the definitions for ALS, AHS and Almost
Fish strong inferences: each one has a candidate, or set of candidates,
which if removed cause a logical structure to become valid. This gives us a
strong inference with the removed candidates on one side and the resulting
structure on the other side. Can we do this with other logical structures,
such as ALC, MSLS, Sue-de-Coq, even other AIC?
Yes we can. However there isn't much information online on this so I'll
have to advance my own standards and notation. Keep in mind everything in
this section is my own conception of Almost-AIC, born of months of
experimentation and a couple of failed attempts at formalising branching
chains into AIC (my older articles have lots of very very ugly awful moves
because I wasn't as good at finding them yet). There are undoubtedly other
solvers out there with their own procedures, this is just the
conceptualisation that works best for me.
Let's step back and examine our understanding of AIC so far. AIC is formed
by constructing chains via inferences between premises. If these inferences
are valid then the AIC is automatically valid and proves that the endpoint
premises have a strong inference, and in Sudoku we can leverage this new
strong inference to eliminate mutual peers.
If however one of the strong inferences within the chain is invalid, the
AIC is no longer valid and cannot be used to eliminate the candidates. An
example is presented below.

Almost-W-Wing: (2=1)r7c2 - r4c2 = r4c5 - (1=2)r9c5
Most of the AIC checks out but the strong inference (1)r4c2 = (1)r4c5 is
invalid as there's an extra 1 in row 4 preventing these candidates from
being bilocal. We can't assert that both of these candidates can't be false,
because they clearly can, if 1 is in r4c8. As a result these eliminations
are invalid and potentially even incorrect.
Recall that all of the instances of a digit candidate within a single
region form a strong inference set. We can split this strong inference set
into two subsets and as long as the two subsets together contain every
element of the main set, there is a strong inference between these subsets.
Each of the subsets is equivalent to the premise "the location of digit N in
this region is within these cells". Previously we just grouped these by
their mutual row/column/box weak inferences and went on our merry way, but
we don't have to stop the analysis there. We can group these subsets by
their AIC-derived weak inferences.
If I group the strong inference set into the following two subsets:
{1r4c2, 1r4c5} = {1r4c8}
When the left premise is true the strong inference (1)r4c2 = (1)r4c5 is valid and so our AIC is valid. In a sense, the left
premise is equivalent to the premise that the AIC is valid. What we've shown
is that there is a strong inference between this "Almost-AIC" and the
candidates preventing it from being valid.
This has major implications. Any AIC that "almost works" can potentially
have its eliminations rescued by chaining off the extra candidates.
Furthermore, AIC themselves become a premise that we can freely use in
chains, even multiple within the same chain. The weak inferences of an AIC
are simply its eliminations: both cannot be true at once for obvious
reasons.
I like to call the candidates preventing the AIC from being valid the
"Kraken candidates". It's a term derived from Fish, referencing the mythical
Kraken with its many tentacles. I'd say it's accurate here as Kraken AIC
tend to branch out across the entire grid, although the overall structure of
the AIC is still linear.
When it comes to notation, I like to enclose the Almost-AIC in [square
brackets] with the Eureka notation of the Almost-AIC included within. Other
than that there's nothing too special, the rest looks like any other linear
AIC. In diagrams I tend to colour the Kraken candidates in grey and I don't
draw the strong inference between the AIC and its Kraken candidates because
it makes things messy.
Here's a slight modification to the example above allowing one of the
eliminations to be rescued.

(4)r7c6 = (4-3)r7c8 = (3-1)r4c8 = [(2=1)r7c2 - r4c2 = r4c5 - (1=2)r9c5] => r7c6<>2
This AIC proves that the endpoints have a strong inference, (4)r7c6
= [(2=1)r7c2 - r4c2 = r4c5 - (1=2)r9c5]. At least one is true so we may
eliminate all mutually eliminated candidates. The only candidate eliminated
by both the W-Wing and (4)r7c6 is (2)r7c6.
Here are some examples from real puzzles.

[(7=8)r3c6 - r13c5 = r7c5 - (8=7)r7c3] = (8)r5c5 - (8=14)r6c46 -
(4=2597)r1256c1 => r3c3<>7
This is a Kraken Grouped W-Wing, similar to above.

(5)r4c5 = [(8=3)r4c5 - r18/c15 = r1c9 - (3=8)r3c8] - (8)r4c8 = (8-5)r6c9 =
(5)r5c79 => r5c6<>5
The candidates of a cell can be used as a strong inference set in this
manner too. In this example there's a strong inference between (5)r4c5 and
(38)r5c4 and the latter is used in an Almost-AIC (actually another W-Wing
variant containing a Kraken X-Wing).

[(1=4)r8c5 - r8c1 = r3c1 - (4=1)43c2] = [(4=5)r4c2 - (5=8)r3c2 - r3c6 =
(8-6)r2c6 = (6)r4c6] - (4)r4c6 = r7c6 - (4=1)r8c5 => r8c2<>1
The strong inference set (1458)r3c2 is divided into two groups, (14) and
(58). Each of these groups has an associated Almost-AIC. (14) gives us a
W-Wing and (58)'s weak inferences can be chained off in order to reach
around to the W-Wing eliminations. I've coloured the sets in blue and purple
respectively to make the diagram easier to read.

(789)r5c6 = [(1=2)r9c6 - r7c5 = (2-49)r5c5 = (4-1)r9c5 = (1)r45c5] =>
r5c6<>1
In this example the potential Unique Rectangle (12)r59c56 has 6 guardians,
forming a strong inference set. This strong inference set can be divided
into two subsets:
{7r5c6, 8r5c6, 9r5c6} = {4r5c5, 9r5c5, 4r9c5}
The latter of which gives us the AIC (1=2)r9c6 - r7c5 = (2-49)r5c5 = (4-1)r9c5 = (1)r45c5 by grouping the
candidates according to their common cells.
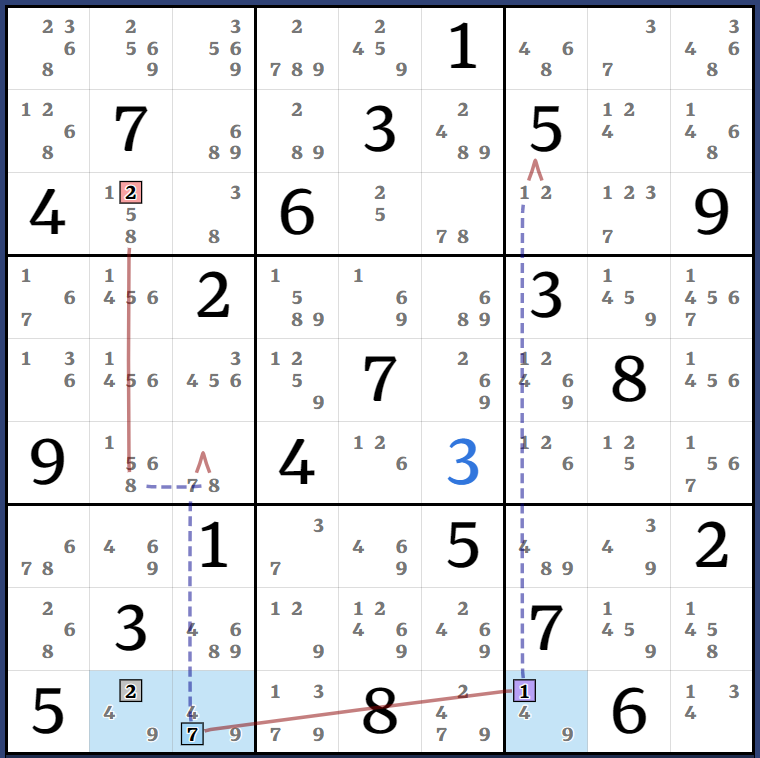
(2)r9c2 = [(8)r3c2 = r6c2 - (8=7)r6c3 - (7=491)r9c237 - (1=2)r3c7] =>
r3c2<>2
In this example the Kraken candidate is an AALS digit. Recall that an ALS
is formed by N cells in a region that contain N+1 unique candidate digits,
and there is a strong inference between every pair of digits.
An AALS is formed by N cells in a region that contain N+2 unique candidate
digits, and every triplet of digits forms a strong inference set.
This strong inference set can be grouped and used in Almost-AIC. This can be
generalised to AAALS, AAAALS, etc. for strong inference sets of quadruplets
and quintuplets respectively.
The same property extends to AAHS - every triplet of cells forms a strong
inference set.

[(2=5)r4c2 - r2c2 = r2c3 - (5=2)r9c3] = (5)r2c7 - (5)r8c7 = [(2=6)r8c7 -
(6=52)r89c3] => r8c2<>2
Here's a delightful move which I like to call a "tie". We have a W-Wing
which is almost valid save for (5)r2c7, and an XYZ-Wing which is almost
valid save for (5)r8c7. Both of these Kraken candidates are in the same
column so both cannot be true at once, therefore at least one of the AICs
must be valid. This Almost-W-Wing and Almost-XYZ-Wing are thus tied together
and their mutual eliminations may be removed. It's really the simplest AIC,
A = B - C = D => A = D, except A and D are both Almost-AIC
premises.
Blossom Loop
Over on the Chinese internet the high-level Sudoku solvers have also been
developing their own theories of branching chains. It's hard for me to know
the full story as there's a significant language barrier but they refer to
Almost-AIC as "Burring Chain", where the chain is the AIC, and the Kraken
candidate is referred to as the "Burr", sometimes "Thorn". You can find a
great wealth of information about the topic in this Baidu group and particularly in this bilibili collection.
One of these Burring Chain techniques is the Blossom Loop, which has been brought to the English-speaking Sudoku sphere by
YZF.
Recall that when chaining, an Almost-AIC's weak inferences are simply its
eliminations. Most AIC will only eliminate one or two candidates so it can
be difficult to get everything to line up and lead to mutual eliminations.
The exception to this is Rings - Rings can have a multitude of eliminations,
even dozens. Chaining off Almost-Rings is a good strategy that can reward
you with easier eliminations.

(7)r6c7 = (7-1)r1c7 = r1c4 - r3c5 = (1-7)r4c5 = (7)r6c5- =>
r1c7<>238, r3c4<>1, r4c5<>2, r6c2<>7
Unfortunately this potential Ring is invalid because column 7 contains an
extra 7. We can declare (7)r2c7 the Kraken candidate and attempt to build an
AIC that rescues the potential Ring eliminations.
While doing this you may run into a situation where the Kraken end node is
one of the potential eliminations of the Almost-Ring, meaning they share a
weak inference. This makes the entire AIC a Ring, including the internal
almost-Ring itself.

[(7)r6c7 = (7-1)r1c7 = r1c4 - r3c5 = (1-7)r4c5 = (7)r6c5-] = (7)r2c7 - r2c12
= (7-9)r1c1 = r1c2 - (9=7)r6c2- => r1c7<>238, r3c4<>1, r4c5<>2, r1c1<>38,
r49c2<>9
This rare technique is called the Blossom Loop. Any strong inference set
can be used for this process - YZF's solver has region, cell and AALS
variants implemented.

[(3=14)r7c78 - r5c7 = (4-3)r4c9 = (3)r9c9-] = (7)r7c8 - r7c23 = (7-5)r8c2 =
r8c1 - (5=238)r126c1 - r6c9 = (8)r4c9- => r7c5,r8c8<>1,
r4c9<>29, r7c4<>7, r8c2<>8, r4c1<>2
Here we have an AALS Blossom Loop built off the strong inference set
between the three AALS digits 3, 4 and 7. As this is a Ring all weak
inferences become strong, all strong inferences become weak, all that is
solid melts into air, all that is holy is profaned, and the remaining ALS
digits (in this case it's just 1) are locked into the ALS, so we can remove
all 1s that see the ALS, just like in standard Rings.
---
You've reached the end of the article. Thanks for reading. Applying every
technique as described up to this point will solve almost every puzzle up to
~9.3 SE. This point represents the extent of my current Sudoku solving
capacity, and unless there's an MSLS, Exocet, etc. to lower the difficulty
it's unlikely I'll be able to crack the harder puzzles without extensive
trial and error.
The next step up would be to implement Almost-Almost-AICs but these take
absolutely forever to search for manually and I imagine they would even slow
down a modern computer. I wonder how many "Almost"s you need to solve any
puzzle without fail.
I have some ideas for generalising the "Almost" process into grouped strong
inference sets based on common AIC-derived weak inferences and iteratively
applying this to get the "Almost-Almost", "Almost-Almost-Almost"-AICs etc.,
once I've coded it up I'll revisit the relevant section of this
article.



Comments
Post a Comment