Solving "Impossible #1" with DoF>1 AIC

I've been learning advanced Sudoku tactics for about 2 years now and lately I've been venturing into the world of branched AIC. It's very work-intensive to identify useful examples, but the results are equally rewarding.

In this post I'll be solving the puzzle "Impossible #1" by the Sudoku.Coach user "Public github database". I don't know what their username is about, I couldn't find this puzzle on Github or anywhere else, and they have yet to post another puzzle - but it was an interesting solve nonetheless. 

You may play the puzzle here: https://sudoku.coach/en/s/6gcT

Of course there are spoilers below, so now's the time to try it yourself if you're interested in doing so.

Required knowledge for this article: AIC, Rings, ALS, ALC, UR, the ability to research terms you don't understand.

There are a lot of images so I kept them small, click to enlarge if you want to see the details.

Quick overview of the difficulty

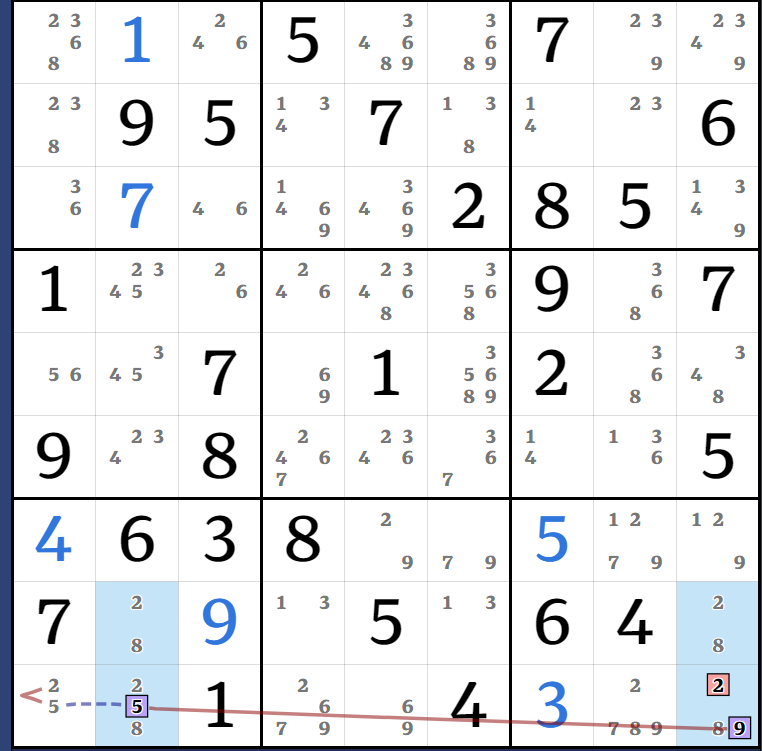
Puzzle string: 000500700095070006000002850100000907007010200908000005063800000700050640001004000

SE: 9.0

YZF has to apply a few Forcing Chains to bring it down to a manageable enough level that the AIC solver can take a crack at it. Indeed it was presented to me as "not quite impossible... but requires 23 forcing chains".

Despite that this is still within reach of AIC if you extend your understanding to encompass higher Degrees of Freedom. In a typical AIC your nodes are connected by strong links two at a time. Every link has a Degree of Freedom of 1. These pairs of nodes are then connected by weak inferences, creating a chain where logical inferences propagate out from either end and prove that at least one end of the chain must be true. 

Here's an example from another puzzle:

(2)r4c5 = (2-4)r6c5 = (4-8)r6c7 = (8)r4c9 => r4c9<>2

Both ends of the chain see 2r4c9 so it may be eliminated. Here's a Grouped AIC:

(2)r5c9 = r4c89 - r4c5 = (2-4)r6c5 = (4)r6c7 => r5c9<>4

You'll notice one of these nodes is actually composed of 2 cells: it doesn't matter as long as the strong and weak links emanating from it are still valid. The strong link r5c9 = r4c89 has a DoF of 2 but the link still holds because all the nodes cannot be false at once (b6 would not contain a 2). And the weak link r4c89 - r4c5 still holds because at most one of the nodes can be true at once. There's a split in the chain but it still works out in the end, and the grouped cells work as one cell under this context. The ends of the chain are still connected by a series of alternating strong and weak links.

Note this branch-splitting behaviour only applies to the strong links.

There are other examples like ALS, AHS, Fish, Fireworks etc. as links with more complicated rules for which nodes can or cannot be true at once but let's return to the original puzzle and talk about branched chains.

First step of the solution is a short X-Chain, (4)r2c4 = r2c7 - r6c7 = (4)r5c9 => r5c4<>4 

Second step is where it gets interesting. 

Kraken Row: (2)r6c5 = [(2)r9c1 = r89c2 - r6c2 = (2-7)r6c4 = (7-6)r9c4 = (6)r9c5] => r9c5<>2

You'll realise I greyed out 2r6c5 because I originally postulated this as an "Almost AIC". This AIC (2)r9c1 = r89c2 - r6c2 = (2-7)r6c4 = (7-6)r9c4 = (6)r9c5 is almost correct, save for the 2r6 strong link containing 3 nodes rather than 2. However, the errant 2 would also eliminate 2r9c5, so we can get away with it. If I draw out the graph in the same way as above:

All ends of the AIC can be reached from the other ends via alternating strong and weak links and all ends eliminate 2r9c5. This is called a "Kraken Row" because the row has 3 branches (heads?) emanating from it. You'll also find Kraken Column, Kraken Cell, etc.

The "almost AIC" framing helps when you put it down to notation: the AIC that almost works is contained in square brackets, and outside the brackets we have the third branch of the chain which is strongly linked to the rest. Keep this in mind because it's all going to get stretched in the next step.

Almost ALC:

(1)r3c9 = (1-69)r3c4 = [(9)r13c5 = (9-6)r1c6 = r13c5 - (6=9)r9c5-] - (9=2)r7c5 - (2=13)r8c46 => r8c9<>1

First off here's the potential ALC we're chaining off of:

It forms a rank0 Ring so we can treat the weak links as strong links for eliminations - and for chain extensions. Breaking down the Eureka notation, within the square brackets is the ALC, to the left is the Kraken chain extension, to the right is a transport.

Purple box is the ALS (123)r8c46. There are two Kraken strong links here but they are neatly tied up by the grouped link (1-69)r3c4. It all comes together and you can traverse from end to end.

We have some more straightforward steps I'll speed through.

XYZ-Ring: r2c47 & r8c4 connected by 1r3

UR AIC: (2=5)r9c1 - (5)r9c2 = (9)r9c9 => r9c9<>2

UR AIC: (1=4)r2c7 - (4)r2c4 = (8)r2c6 => r2c6<>1

UR AIC: (4)r2c4 = (8)r2c6 - (8=23)r2c18 => r2c4<>3

Almost ALC: (6=9)r9c5 - (9)r7c6 = [(6=9)r5c4 - r5c6 = (9-6)r1c6 = r456c6-] => r46c5<>6

Same principle as before! After this point the puzzle has been reduced to an SE of 8.4. Still hard but we won't require branched chains from now on.

X-Chain: (2)r6c5 = r6c2 - r8c2 = r8c9 - r7c89 = (2)r7c5 => r4c5<>2

ALS-AIC: (7)r6c4 = r9c4 - r9c8 = (7-1)r7c8 = r6c8 - (1=234)r6c257

ALC Triple

Two-String Kite

Empty Rectangle/X-Chain

X-Chain

XY-Wing

Skyscraper

ALS-XZ

ALS AIC: (6=372)r6c456 - r6c2 = (2-6)r4c3 = (6)r5c1 => r5c46<>6

STTE

There we go :D An SE 9.0 puzzle which would normally not be solvable with AIC, brought to its knees because we expanded our definitions a little bit. Branched chains are very powerful. 

I'll write more blog posts like this whenever I have more solutions to share. I recommend keeping up with the EnjoySudoku forums: http://forum.enjoysudoku.com/puzzles-f33.html

Or r/Sudoku on Reddit, where there are many things to look out for. People often post puzzles asking for help - sometimes they have an SE above 7 and result in interesting solutions. 

There are also weekly challenge threads, here is this week's, containing some discussions on Tridagons and MSLS: 

https://www.reddit.com/r/sudoku/comments/1jhqak9/weekly_sudoku_puzzle_challenges_thread/

Some posters to watch out for:

u/strmckr

u/Special-Round-3815

u/SeaProcedure8572

u/shye_

u/Nacxjo

u/Neler12345

u/numpl_npm

They all begin with S or N.