Sudokuwiki.org's Weekly 'Unsolvable' Sudoku #640
In this post I'll be tackling the weekly "Unsolvable" puzzle from SudokuWiki. This week's puzzle was provided by Richard Kröger, as with last week's.
Puzzle string: .....8.7.....5...9...2.43...8..4..6.5....3.....27....19....6..5..7.1..8..3....4..
SE: 9.2
It turns out 9.2 is way harder than 9.0, so buckle up, we're going to be here for a while.
No basics to start off with, it's straight into the fire.
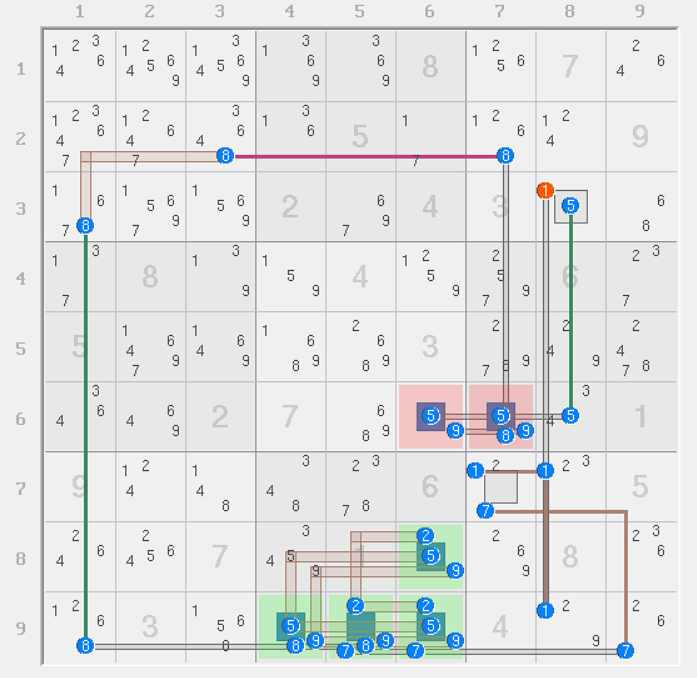
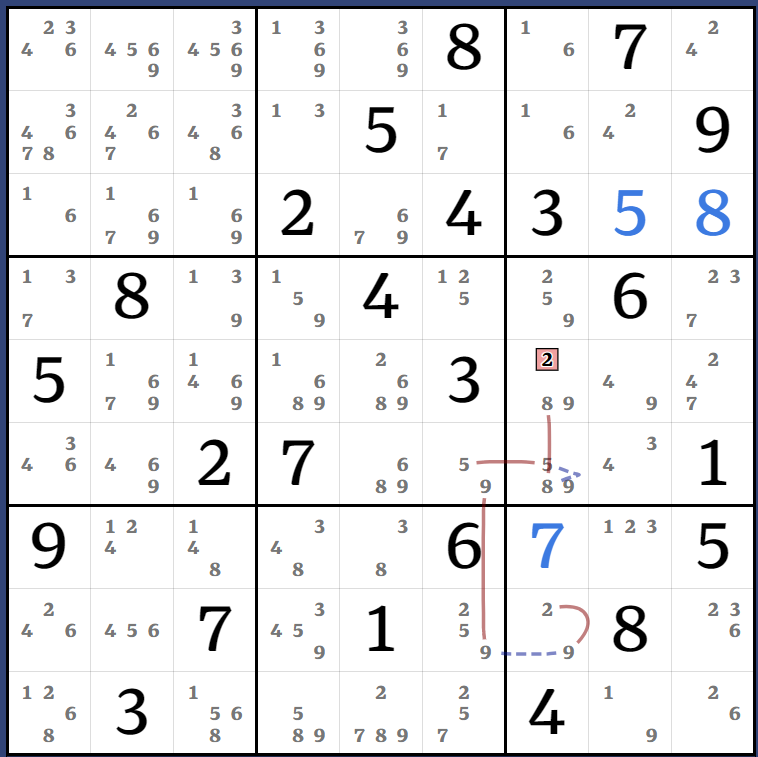
[(9=5)r6c6 - (5=9)r8c6 - r8c7 = (9)r456c7] = (2)r8c6 - (2)r4c6 = [(9=5)r6c6 - r4c46 = (5-2)r4c7 = (2-3)r4c9 = (3)r6c8] => r6c8<>9
If you're unfamiliar with my use of almost-AICs you may want to read this post before proceeding. This elimination comes from two chains that "almost" eliminate 9r6c8, save for one of the strong links in each having 3 nodes rather than 2 - but these extraneous nodes are actually both contained within the same column, so they cannot both be true at once, hence the AICs cannot both be false at once.
The Almost-AIC here (6=241)b7p234 - r9c13 = (1-9)r9c8 = (9)r8c7 would eliminate 6r8c7. With a bit of transporting we can get a usable elimination from this + the extra 8.
The Almost-AIC is pretty large, here's a screenshot of it in Xsudo:
Still haven't found a good opportunity to reuse any of these virtual strong links (this one would be 8r2c1 = 5r3c8).
(5)r8c2 = r9c3 - (5)r9c46 = [(1=2897)r9c4568 - r9c9 = (7)r7c7] - (1)r7c7 = r2c7 - (1=5)r3c8 => r3c2<>5
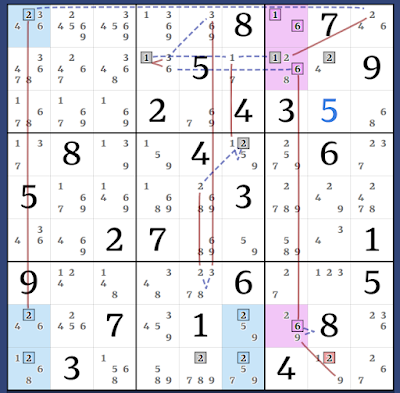
AAAHS-AIC: (9)r1c2 = [(1)r3c123 = r3c8 - r79c8 = (1-7)r7c7 = r7c5 - r9c6 = r2c6 - (7)r2c2 = [(5)r3c8 = (5-3)r6c8 = r4c9 - (3)r4c13 = [(7=19)r4c13 - r56c2 = (9-7)r3c2 = r56c2 - (7=19)r4c13-] - (1)r4c6 = (1-7)r2c6 = r9c6 - r7c5 = (7-1)r7c7 = (1)r79c8] - r3c8 = (1)r3c123] => r1c2<>1
This is such a mouthful but I'll break it down, it's not as complex as it looks. This is an Almost-Almost-AHS AIC. I'm still working out my notation system as I go but in general I've tried to keep Kraken links on the left and transports on the right. The AALS I've marked in blue is being "reinforced" by the purple AHS because the Almost-ALC here shows that the ALS cannot contain both 7 & 9. It's very hard to put this into notation and I don't think my attempt was entirely correct. Either way it effectively proves a strong link (1)r4c13 = (3)r4c13 which we can use to build the AIC below:
The Kraken digit (7)r2c2 can be reincorporated into this AIC easily with (7)r2c2 - r2c6. Then we just have the loose ends (9)r1c2 and (5)r3c8, which give us the elimination (9)r1c2 = (5-1)r3c8 = (1)r3c123 => r1c2<>1. Perhaps the graph diagram makes it clearer:
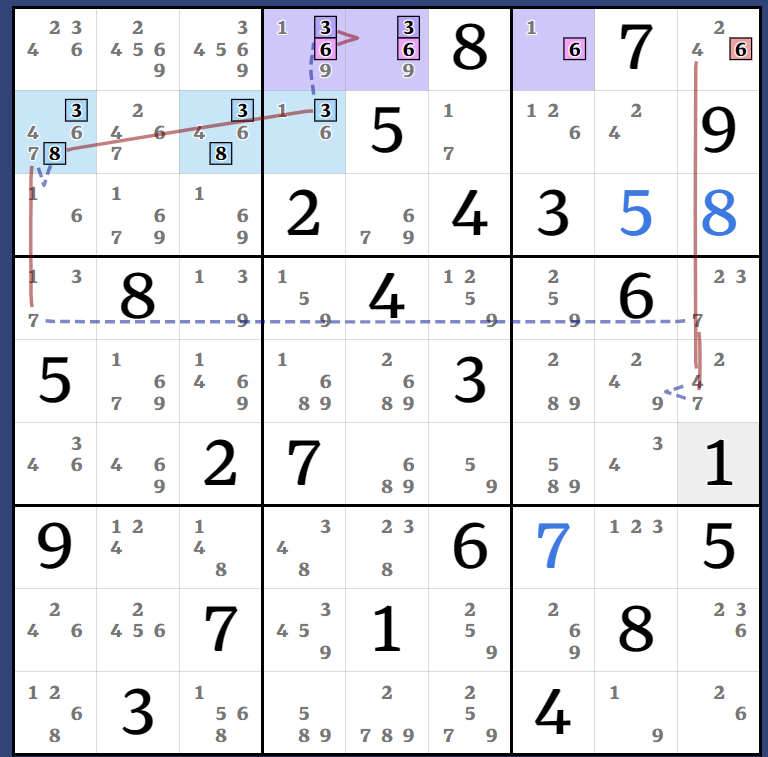
AAAHS-AIC: (1)r3c123 = (1-5)r3c8 = (5-3)r6c8 = r4c9 - (3)r4c3 = [(1)r3c123 = (1-5)r3c8 = (5-3)r6c8 = r4c9 - r8c9 = (3-4)r8c4 = r8c12 - (4)r7c3 = [(1)r3c123 = (1-5)r3c8 = (5-4)r6c8 = r6c12 - (4)r5c3 = (34)r12c3]] => r1c3<>1
Another Almost-Almost-AHS where every Kraken candidate leads nicely into the same AIC. This one has a long Eureka notation but so much of it is redundant. The graph is much neater:
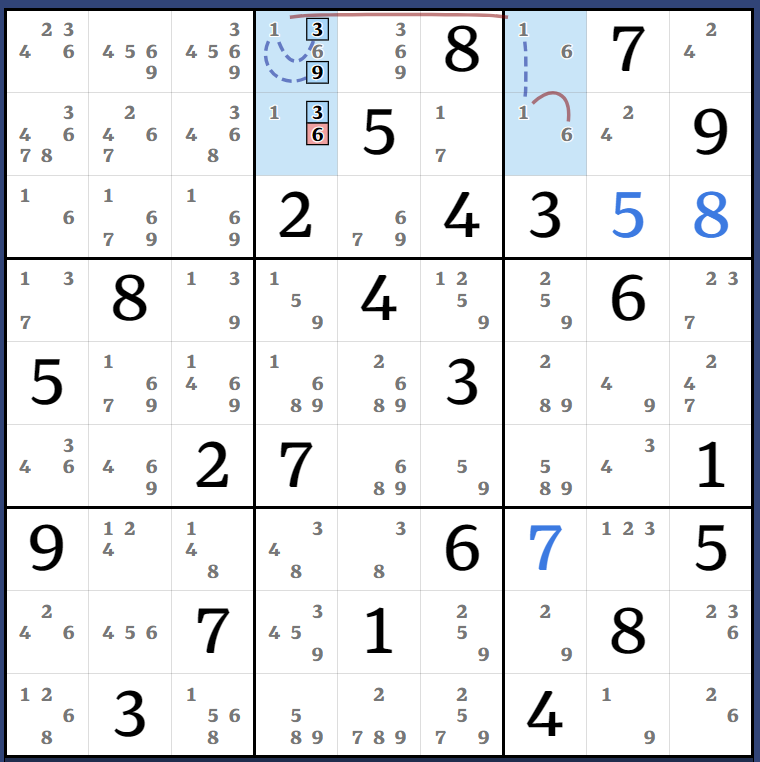
(1)r2c4 = [(1)r3c123 = (1-5)r3c8 = (5-6)r1c3 = [(1)r3c123 = (1-5)r3c8 = r1c7 - r46c7 = r6c8 - (5=9)r6c6 - (9)r8c6 = [(1)r3c123 = (1-5)r3c8 = r1c7 - r46c7 = (5-3)r6c8 = r7c8 - r7c45 = (3-9)r8c4 = (9-6)r8c7 = r2c7 - (6=3)r2c4 - r78c4 = r7c5 - r7c8 = (3-5)r6c8 = r46c7 - r1c7 = (5-1)r3c8 = (1)r3c123]]] => r2c2<>1
3 Kraken candidates in this one. And so much overlap! I didn't want to make more graph diagrams but I have to, the amount of retreading in this chain is quite absurd. I think this is just what happens when you start abusing Kraken links like this, especially on a grid with so few natural strong links to use.
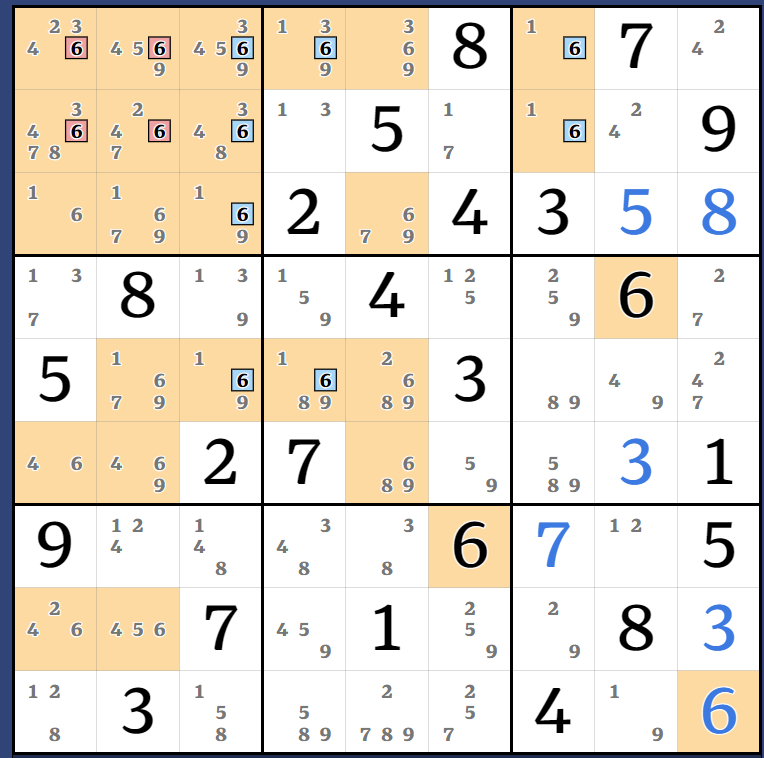
Traverse this graph only by alternating between red & blue lines and you'll end up at the 1r3c123 or 1r2c4 branches no matter what. In short: (1)r2c4 = (5)r3c8. Side note: this chain eliminates r2c123, and I could have used it earlier to save myself a lot of work, ouch! But we're almost done picking away at the 1s in box 1.[(1)r3c123 = (1-5)r3c8 = (5-3)r6c8 = r4c9 - r8c9 = (3-4)r8c4 = r7c4 - (4=1)r7c3 - r9c13 = r9c8 - r3c8 = (1)r3c123] = (8)r7c3 - (8)r2c3 = [[(2)r1c1 = (2-8)r2c1 = r2c7 - (8=95)r6c67 - r6c8 = (5-1)r3c8 = (1)r3c123] = (2)r89c1 - (2)r7c2 = [(1)r9c8 = r9c13 - (1=4)r7c2 - r7c4 = (4-3)r8c4 = r8c9 - r4c9 = (3-5)r6c8 = (5)r3c8] - (1)r3c8 = (1)r3c123] => r1c1<>1
AIC-tie-(AIC-tie-AIC). There are 3 Almost-AIC here connected by 8c3 and 2b7 weak links, again with lots of overlap. This elimination allows us to set our first digit, 5r3c8. However it does not help the solve much, and it is rapidly becoming clear to me that I'm exhausting my options - these eliminations aren't earning me any useful strong links and I'm having to use more and more Kraken candidates to keep everything coherent. Also, most of my chains up to this point used r3c8 in some way, but I can't do that any more. I got stuck after this stage for about 4 hours, only finding another fairly useless elimination while searching for multi-digit Fish out of desperation.
(4)r6c12 = r6c8 - (4)r2c8 = [(4)r6c12 = (4-3)r6c8 = r6c1 - r4c13 = r4c9 - r8c9 = (3-4)r8c4 = [(4)r6c12 = (4-3)r6c8 = r6c1 - (3)r248\c1349] = (3-4)r2c3 = (4)r28\c12] => r5c2<>4
All the truths here are in rows so you could describe this as a 2-digit Finned Franken Fish. At its core is the mutant X-Wing (4)r28\c12 which has 3 Kraken candidates. 2 of them easily lead to (4)r6c12, the last can be tied to an Almost-Finned Swordfish via (4-3)r2c3 = (3)r248\c1349.
(7)r7c7 = r9c9 - (7)r5c9 = [(1)r12c7 = (1-4)r2c8 = r56c8 - (4=2)r5c9 - r5c5 = (2-1)r4c6 = r2c6 - r2c8 = (1)r12c7] = (8)r5c9 - r6c7 = (8-6)r6c5 = [(1)r12c7 = r2c8 - r2c6 = (1-2)r4c6 = (2-6)r5c5 = r5c4 - (6)r2c4 = [(1)r12c7 = r2c8 - (1=3)r2c4 - r1c5 = (3-7)r7c5 = r9c56 - r9c9 = (7)r7c7]] => r7c7<>1
Kraken Cell tie Almost-AIC. All roads lead to Rome, or in this case 1r7c7.
Kraken Cell: (2=4)r2c8 - (4)r5c8 = [(2=5789)r4567c7 - (9=2)r5c8 - r5c5 = (2-1)r4c6 = r45c4 - r1c4 = (1)r1c7] => r1c7<>2
AIC tie AHS-AIC: [(2)r2c78 = r1c9 - (2=3)r4c9 - (3=4)r6c8 - (4=2)r2c8] = (7)r4c9 - (7)r4c1 = [(7)r2c1 = r3c1 - r3c5 = (7-1)r2c6 = r4c6 - (1)r4c1 = (178)r239c1] => r2c1<>2
(2)r2c8 = [(2)r9c5 = [[(9)r9c8 = (9-6)r8c7 = (16)r12c7 - (2)r2c7 = r1c9 - r1c1 = (2)c16\r89] = (2-1)r4c6 = r2c6 - (1)r2c47 = [(9)r9c8 = (9-6)r8c7 = (16)r12c7 - (6=3)r2c4 - r1c5 = (3-2)r7c5 = r5c5 - (2)r4c6 = [(9)r9c8 = (9-6)r8c7 = (16)r12c7 - (2)r2c7 = r1c9 - r1c1 = (2)c16\r89]]] => r9c8<>2
Not sure if my notation is entirely accurate but you get the gist. 2 of the Kraken candidates directly see r9c8 so we can ignore them. We would have the Kraken X-Wing (9)r9c8 = (9-6)r8c7 = (16)r12c7 - (2)r2c7 = r1c9 - r1c1 = (2)c16\r89 if not for (2)r4c6 so (2-1)r4c6 = r2c6 - (1)r2c46 removes the Kraken candidates of the 2nd AIC. Moving on - I set my sights on 2r7c7 because it seemed really close to being eliminated. There's a lot of strong links connecting to (7)r7c7=r9c9, 2c8 & c6 etc. Setting another digit would be good progress on the puzzle too and make me feel less like I'm digging away at a mountain with a toothpick. Here's what I came up with:
For the sake of visual clarity I'm going to hide the chains for the Kraken candidates. Here's our Almost-AIC:
(2)r7c8 = (2-4)r2c8 = r1c9 - (4=8)r5c9 - r6c7 = r6c5 - (8=9)r9c5 - (9=6)r3c5 - (6=8)r3c9 - (8=4)r5c9 - r1c9 = (4-2)r2c8 = (2)r7c8
These Kraken candidates are in order (I cannot be bothered to write the whole chain out):
(7)r3c5 - r2c6 = r9c6 - r9c9 = (7)r7c7
(2)r5c89 - r5c5 = (2-1)r4c6 = (1-7)r2c6 = r9c6 - r9c9 = (7)r7c7
(7)r5c9 - r9c9 = (7)r7c7
(2)r9c5 - r5c5 = (2-1)r4c6 = (1-7)r2c6 = r9c6 - r9c9 = (7)r7c7
(7)r9c5 - r9c9 = (7)r7c7
=> r7c7<>2
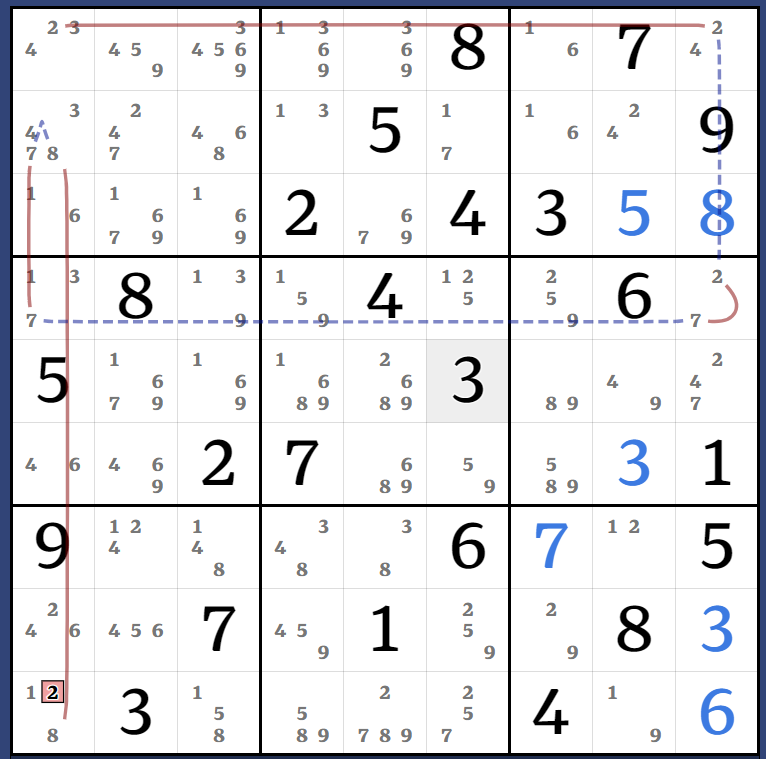
(7)r2c12 = (7-1)r2c6 = r4c6 - (1)r4c1 = [(7)r4c1 = r4c9 - (7)r5c9 = [(8)r3c1 = r3c9 - (8)r5c9 = [(1)r3c1 = r9c1 - (1=9)r9c8 - (9=42)r5c89 - r4c79 = (2-1)r4c6 = (1-7)r2c6 = (7)r2c12]]] => r3c1<>7
Kraken Cell: (8=6)r3c9 - r89c9 = (6-9)r8c7 = r9c8 - (9)r9c5 = [(8)r6c7 = r6c5 - (8)r9c5 = [(8=6)r3c9 - (6=2)r9c9 - (2=7)r9c5 - r3c5 = r3c2 - r5c2 = (7)r5c9]] => r5c9<>8
This sets 8r3c9. The moves have been getting simpler and simpler, I'm hoping the light at the end of the tunnel isn't an incoming train.
AHS-ALS-AIC: (4)r1c9 = (4-7)r5c9 = r4c9 - r4c1 = (7-38)r2c1 = (38)r2c34 - (3=196)r1c457 => r9c1<>6
X-Wing (2)r27\c28
Almost-ALS-AIC: (9=52)r68c6 - r4c6 = r5c5 - (2)r5c7 = [(9=52)r68c6 - r8c7 = (2-5)r4c7 = r4c46 - (5=29)r68c6] => r49c6<>9
(SE=7.3 now)
(3)r4c3 = (3-7)r4c1 = (7-8)r2c1 = (8)r2c3 => r2c3<>3
(2)r1c1 = r1c9 - (2=7)r4c9 - r4c1 = (7-8)r2c1 = (8)r9c1 => r9c1<>2
(2)r1c1 = r1c9 - (2=7)r4c9 - r4c1 = (7-8)r2c1 = (8)r9c1 => r9c1<>2
This was by far the hardest puzzle I've ever solved. I've solved multiple 11 SE before, even 11.9, but they were trick puzzles that relied on obvious Tridagon or MSLS to defuse the difficulty. This was incredibly painful and took me 4 days, from Monday to Friday. Hopefully next week is a bit easier :D

































Comments
Post a Comment