Sudokuwiki.org's Weekly 'Unsolvable' Sudoku #648
In this post I'll be tackling the weekly "Unsolvable" puzzle from SudokuWiki. This week's puzzle was provided by Andrew Stuart.
Puzzle string: .1..8..4...4...8..6..9....7...1.56..7...6...1..13.4...9....6..5..3...2...2..5..8. - Sudoku.Coach
SE: 9.2
Back to the harder puzzles. This one is far more difficult than last week's - it quickly made me regret letting my guard down.
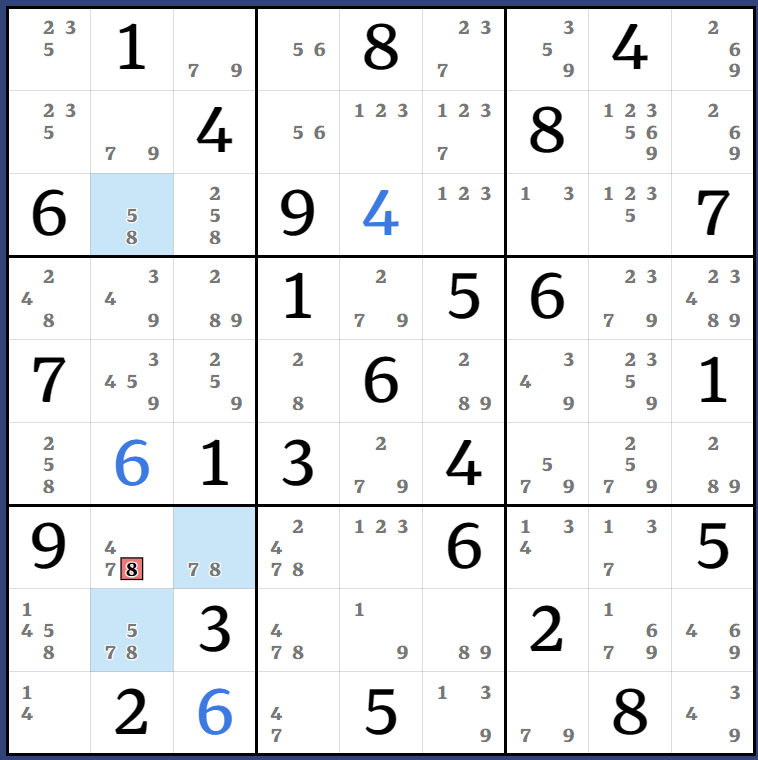
After basics:
(1=9)r8c5 - r89c6 = (9-8)r5c6 = (8)r8c6 => r8c6<>1
Almost-ALC: (8)r6c1 = [(2=5)r6c1 - r5c3 = (5-2)r3c3 = (2)r45c3-] - (8)r3c3 = (8)r3c2 => r4c2<>8
Impossible Pattern AIC: (1)r7c7 = [(5)r8c2 = (5-1)r8c1 =IP= (1-7)r2c6 = (7)r2c2] - (7)r8c2 = r7c23 => r7c7<>7
The impossible pattern here is negative-rank logic in 1r278 - if these guardians were removed there would be 3 rows where 1 is restricted to 2 columns, which is impossible. Wish I could have found more eliminations with this.
Kraken Sue-de-Coq: (5)r6c7 = [(5)r5c3 = r3c3 - (5)r3c8 = [(5)c23\r35 = (5-7)r8c2 = r7c23 - (7)r7c8 = [(7=12359)r34567c8 - (9=7)r6c7-]]] => r5c7<>5
This is an "almost-almost-almost-Sue-de-Coq" because it has 3 Kraken candidates. I'll show the Sue-de-Coq for clarity.
Minus all 3 (plus AHS form as I originally saw it)
Plus 5r3c8, it's easy to salvage the eliminations on 5s with a transport, so really there are only 2 Kraken candidates.
From here the easiest elimination to link up is 5r5c7 as 5r6c7 already sees it. I tried a few more - 5r2c8 seemed most feasible - but none worked out.
Ugly but it works and brings down the puzzle difficulty somewhat. The overlap makes it seem more complicated than it actually is... still quite bad. Think of it as an AAHS with 3 branches: 8r6c9 eliminates 3r3c2 directly, 3r12c9 and 4r8c9 each remove a candidate that validates an AIC to eliminate 3r3c2.
(3)r3c7 = [(3)r7c5 = r2c5 - r3c6 = (3)r3c8] - (3)r7c8 = [(1)r3c7 = r23c8 - (1=7)r7c8 - r7c23 = (7-5)r8c2 = (5)c23\r35] => r3c7<>5
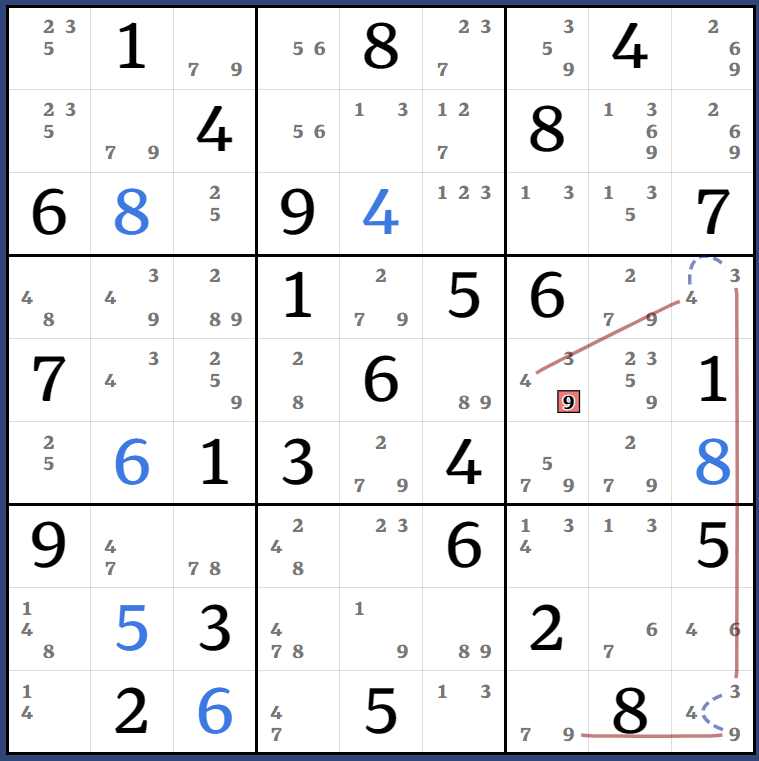
(1)r9c1 = r8c1 - (1=9)r8c5 - r6c5 = r6c789 - (9=341)r357c7 => r9c7<>1
Kraken Row: (7)r9c7 = (7-5)r6c7 = r1c7 - (5)r3c8 = [(4)r5c7 = r5c2 - (4=785)b7p235 - r3c2 = r3c3 - (5=289)r5c346] - (579)(r5c7 = r169c7) => r9c7<>34
(4) - r5c7 = (4-3)r4c9 = r9c9 - (3)
(7) - r7c23 = (7-5)r8c2 = r8c1 - (5=238)r126c1 - r6c9 = (8-3)r4c9 = r9c9 - (3)
Rank0 => r7c5, r8c8<>1, r4c9<>29, r7c4<>7, r8c2<>48, r4c1<>2
XY-Wing
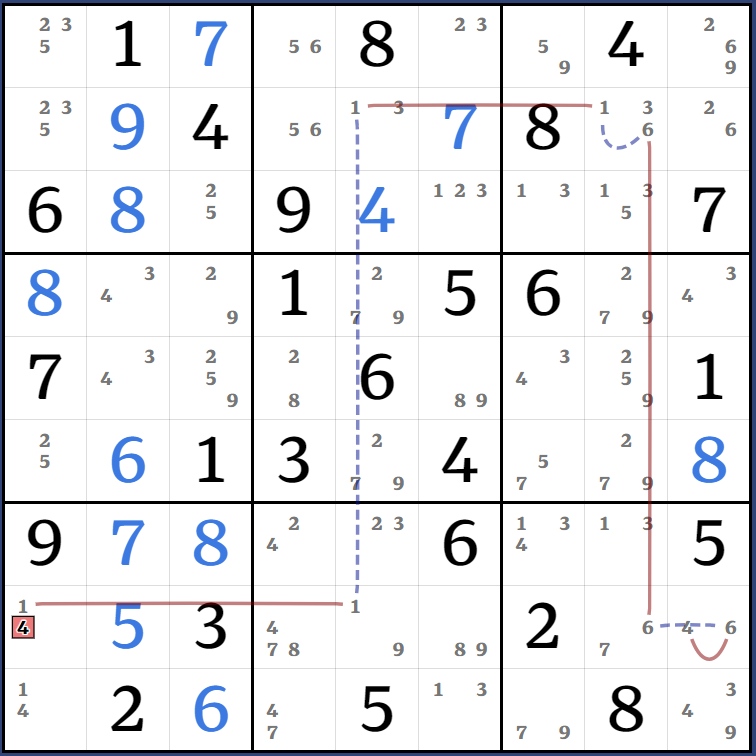
Kraken Row: (7=4)r7c2 - (4)r9c1 = [(7)r9c7 = (7-4)r9c4 = (4)r9c9 - (13)(b9p9 = b9p12)] => r7c8<>7
Triple
X-Wing
Kraken Column: (1)r9c6 = [(4=7)r7c2 - r2c2 = (7-1)r2c6 = r3c6 - r3c7 = (1)r7c7] - (4)r7c7 = r5c7 - (4=3)r4c9 - r9c9 = (3)r9c6 => r9c6<>9
Hidden Pair
(9)r9c7 = (9-3)r9c9 = (3-4)r4c9 = (4)r5c7 => r5c7<>9
(4=6)r8c9 - r8c8 = (6-1)r2c8 = r2c5 - r8c5 = (1)r8c1 => r8c1<>4
STTE
Thanks for reading. Nice to get a harder puzzle from Andrew Stuart this time.





























Comments
Post a Comment