Sudokuwiki.org's Weekly 'Unsolvable' Sudoku #649
In this post I'll be tackling the weekly "Unsolvable" puzzle from SudokuWiki. This week's puzzle was provided by Andrew Stuart.
Puzzle String: 7..........21..4...6...5..3..5.2..9.8.......6.7..3.8..9..87..2...4...6.......4..9 - Sudoku.Coach
SE: 9.1
After basics:
Finned Swordfish
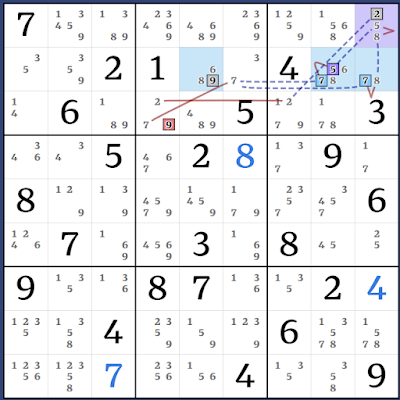
(1=5687)b3p2568 - r3c7 = r45c7 - (7=1)r4c9 => r56c8, r1c9<>1
With an almost-Skyscraper.
Kraken Column: (1=73)r4c79 - (3)r5c8 = [(2)r6c9 = r5c7 - r5c2 = (2-8)r9c2 = (8-3)r9c8 = (3-7)r8c8 = r8c9 - (7=1)r4c9] => r6c9<>1
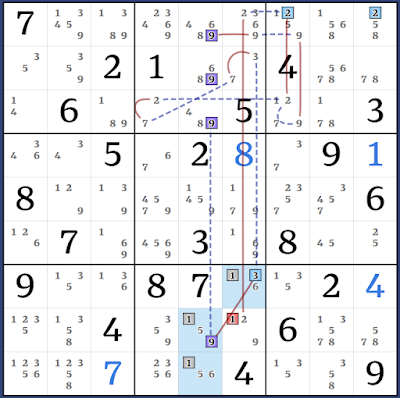
Kraken Row: (9)r3c45 = [(9)r3c7 = r3c3 - r56c3 = (9-2)r5c2 = (2)r5c7] - (2)r3c7 = (2-7)r3c4 = (7)r2c6 => r2c6<>9
Kraken Column: (3)r5c3 = [(3=46)r4c12 - r6c3 = (6-3)r7c3 = r1c3 - r2c12 = (3-7)r2c6 = r3c4 - (7=463)r4c124] => r5c2<>3
(8)r9c8 = (8-2)r9c2 = r5c2 - (29)(r5c7 = r1|3c7) - (1)r1|3c7 = (1)r13c8 => r9c8<>1
Kraken Column: (4=63)r4c12 - (3)r5c3 = [(4=36)r4c12 - r6c3 = (6-3)r7c3 = r1c3 - r1c46 = (3-7)r2c6 = (7-2)r3c4 = r3c7 - r5c7 = (2)r5c2] => r5c2<>4
Getting a lot of mileage out of this 3c3 truth.
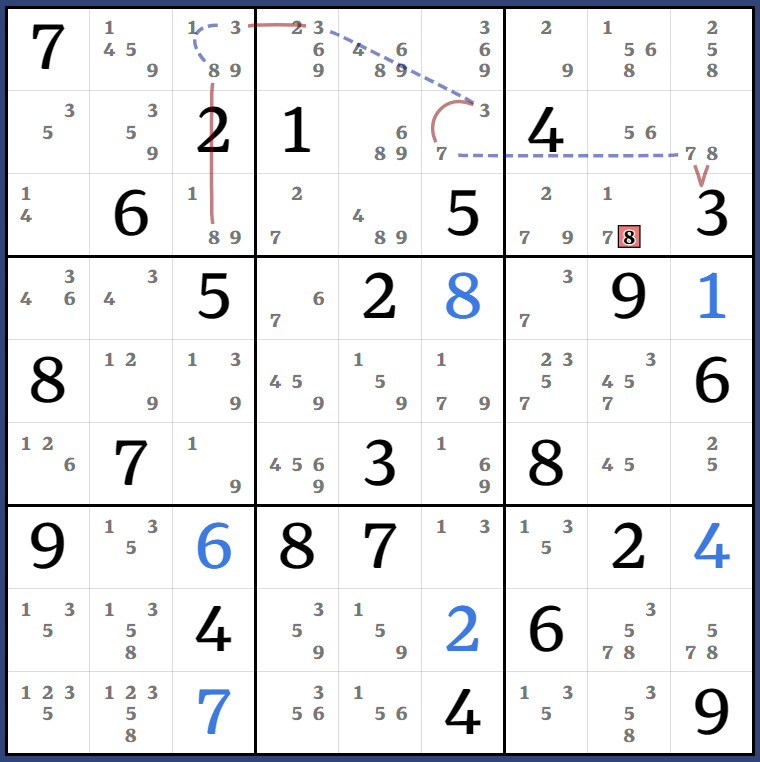
Kraken AAAALS: (5)r1c8 = [(5=3|9)r2c12 - (3|9)r1c3 = [(8=16)r1c38 - r2c8 = (6-8)r2c5 = (8)r2c89] - (8=25)r16c9] => r2c9<>5
Kraken AALS: (2)r3c4 = r3c7 - r5c7 = (2-9)r5c2 = r12c2 - (9)r13c3 = [(4=183)b1p379 - r1c46 = (3-7)r2c6 = (7)r3c4] => r3c4<>4
Kraken Cell+AALS: (9)r2c5 = [(2)r3c4 = r3c7 - (2)r1c9 = [(7=685)r2c589 - (5=8)r1c9 - (8=7)r2c9] - (7)r2c6 = (7)r3c4] => r3c4<>9
(3=7)r2c6 - (7=2)r3c4 - r1c6 = (2)r8c6 => r8c6<>3
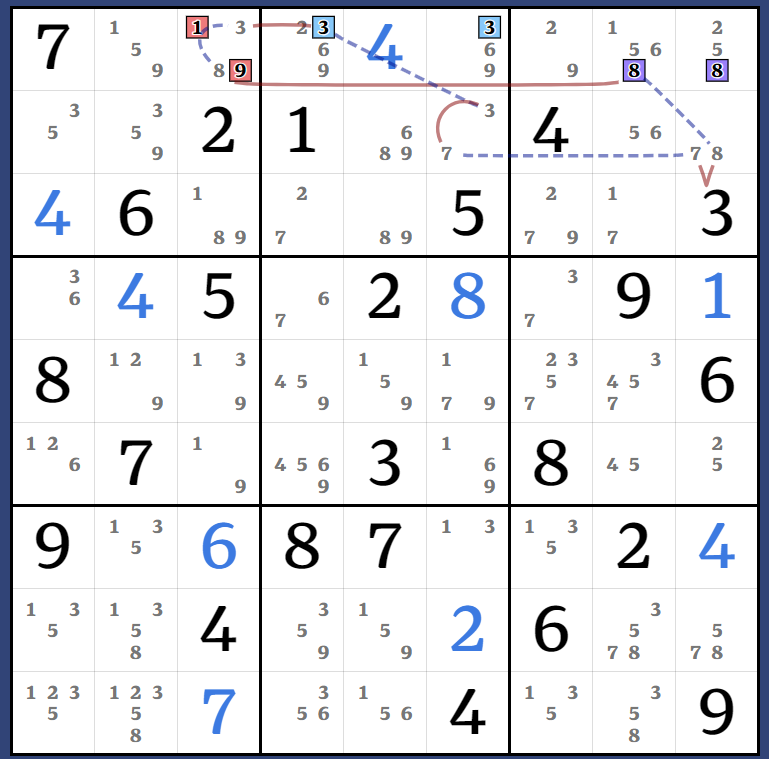
Kraken Column: (4=3)r4c2 - (3)r4c1 = [(4=63)r4c12 - (3)r5c3 = [(4=36)r4c12 - r6c3 = (6-3)r7c3 = r1c3 - r1c4|r2c1 = c14/r89 - r8|9c8 = (3-4)r5c8 = (4)r5c45]] => r4c4<>4
A dodgy one, not very elegant... using the 3c3 truth again, 3r5c3 and 3r7c3 trivially lead to 4 in the ALS r4c12. I was able to find a path connecting 3r1c3 to a shared elimination in r4c4 using a Kraken X-Wing with 2 Kraken candidates being removed at once. 3r4c1 intrudes a bit but it's easily tied up with (3=4)r4c2.
Part of the inspiration for this dual Kraken X-Wing comes from a recent investigation into 4-strong-link patterns that can't be expressed as simple AIC or even Kraken Cell/Regions. There are very few difficult patterns with so few strong links, most are complex Jellyfish or X-Chains, but the rest are Finned/2SK/ER variations of this pattern:
2....7.4..6.5....2....1.9....6..8.719.........5...48...4.8...3...3...2..7....2...
Anyway back to the solve.
Kraken Column: (2)r8c6 = (2-6)r1c6 = [(2)c169/r168 = (2-6)r9c1 = r9c45 - r7c6 = r6c6 - (6=7)r4c4 - (7=2)r3c4] => r8c4<>2
Almost-ALC: (7)c47/r34b6 = (7-4|5)r5c4 = [(4=5)r6c8 - r5c78 = (5-4)r5c5 = (4)r5c8-] - (5=2)r6c9 - (29)(r5c7 = r13c7) - (7)r3c7 = (7)r45c7 => r4c9<>7
Nice this chain is almost entirely linear aside from the ALC (M-Ring). Almost-Finned-Fish are great for simplifying the notation of DoF>1 chains. I think this could have been applied much earlier for a free digit placement.
Kraken Cells: (2)r1c9 = r6c9 - (2)r6c1 = [(2=7)r3c4 - (7=6)r4c4 - (6)r6c6 = [(2=9)r8c6 - (9=1)r6c6 - (1=6)r6c1 - r9c1 = r9c45 - r7c6 = (6)r1c6]] => r1c6<>2
Kraken ALC: (2)r9c1 = (2-1)r6c1 = [(2)r9c1 = r6c1 - r6c9 = r5c7 - r3c7 = (2-7)r3c4 = r45c4 - (7)r5c6 = [(1=9)r5c6 - r6c46 = (9-1)r6c3 = (1)r6c6-] - (6)r6c3 = (6)r46c1] => r9c1<>6
Ring: (3)r1c3 = r5c3 - r4c12 = (3-7)r4c7 = r4c4 - r5c6 = (7-3)r2c6 = (3)r2c12- => r1c2<>3, r5c4<>7
Sashimi X-Wing
(3)r9c4 = r1c4 - r1c3 = r5c3 - r4c1 = (3)r4c7 => r9c7<>3
XY-Wing
STTE
Hooray. Harder than the last few weeks but still not insane for these Unsolvables. Most of the hard moves were simple rank0 structures like ALC with 1 or 2 Kraken candidates that were easily resolved. Also, I noticed early on that the 3c3 truth is very powerful (it's connected to a ton of other strong links across the puzzle). That probably singlehandedly saved me a couple of hours
Comments
Post a Comment