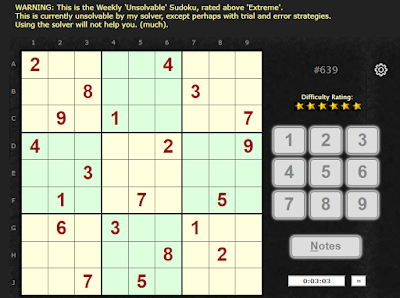
Sudokuwiki.org's Weekly 'Unsolvable' Sudoku #639
In this post I'll be tackling the weekly "Unsolvable" puzzle from SudokuWiki. This week's puzzle was provided by Richard Kröger.
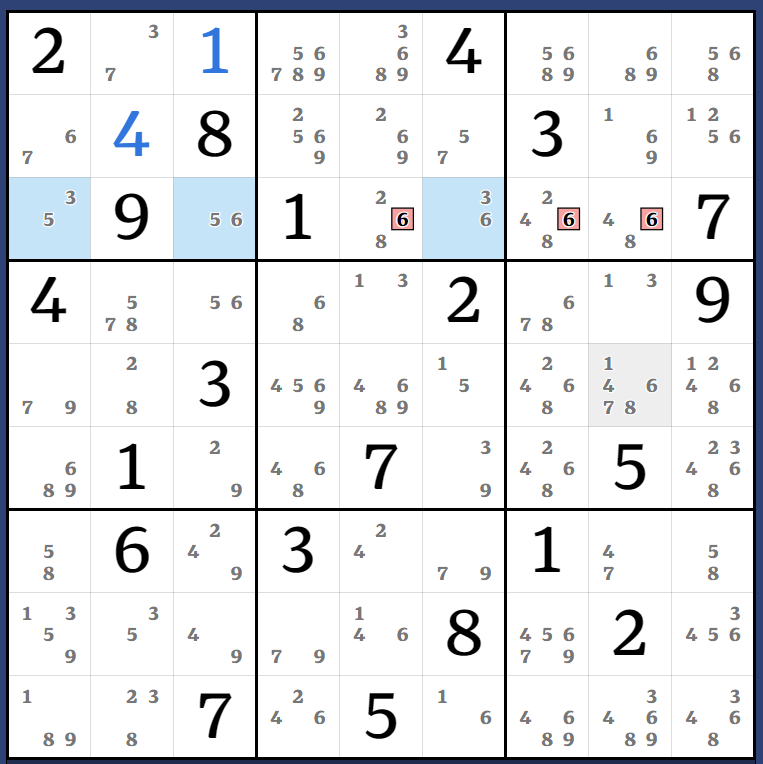
Puzzle string: 2....4.....8...3...9.1....74....2..9..3.......1..7..5..6.3..1.......8.2...7.5....
SE: 9.0
Starting off with basics - click images to enlarge.
Hidden Pair
AIC: (5)r1c7 = (5-7)r8c7 = r8c4 - r1c4 = (7)r1c2 => r1c2<>5
Grouped AIC: (7)r7c8 = (7-5)r8c7 = (5-9)r1c7 = (9)r89c7 => r7c8<>9
Grouped AIC: (9=7)r7c6 - r7c8 = (7-9)r8c7 = (9)r9c78 => r9c46<>9
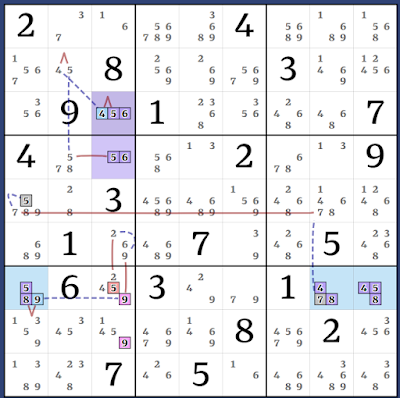
[(3)r6c6 = r3c6 - r1c5 = (3-7)r1c2 = (7-1)r2c1 = r9c1 - (1=6)r9c6] = (1-3)r8c1 = [(3)r6c6 = r6c9 - r8c9 = r8c2 - r1c2 = r1c5 - r3c6 = (3)r6c6] => r6c6<>6
Almost XY-Wing tie Almost ALS-AIC: [(5=4)r2c2 - (4=6)r3c3 - (6=5)r4c4] = (5)r3c3 - (5)r3c6 = [(5)r5c6 = (5-7)r2c6 = r2c1 - (7=3)r1c2 - (3=45)r28c2] => r5c2<>5
(9)r5c1 = r5c456 - (9=3)r6c6 - (3)r3c6 = [(5=4)r2c2 - (4=65)r3c36] - (5)r3c1 = [(7)r5c1 = r2c1 - (7=3)r1c2 - (3=6)r3c1] => r5c1<>6
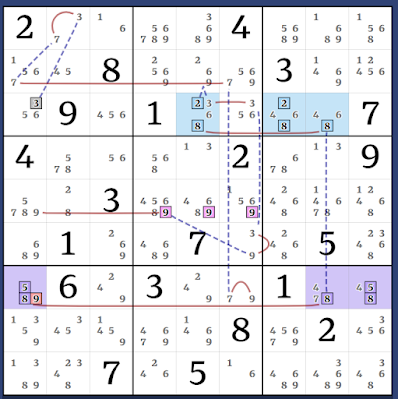
[(9)r5c1 = r5c456 - (9=3)r6c6 - r3c6 = (3-28)r3c5 = (28)r3c78) - (8)r7c8 = (58)r7c19] = (3)r3c1 - (3=7)r1c2 - r2c1 = r2c6 - (7=9)r7c6 => r7c1<>9
Grouped ALS-AHS-AIC: (7)r5c1 = r5c8 - (7=584)r7c189 - (4)r9c789 = (24)r9c24 - (8)r9c2 = r45c2 => r5c1<>8
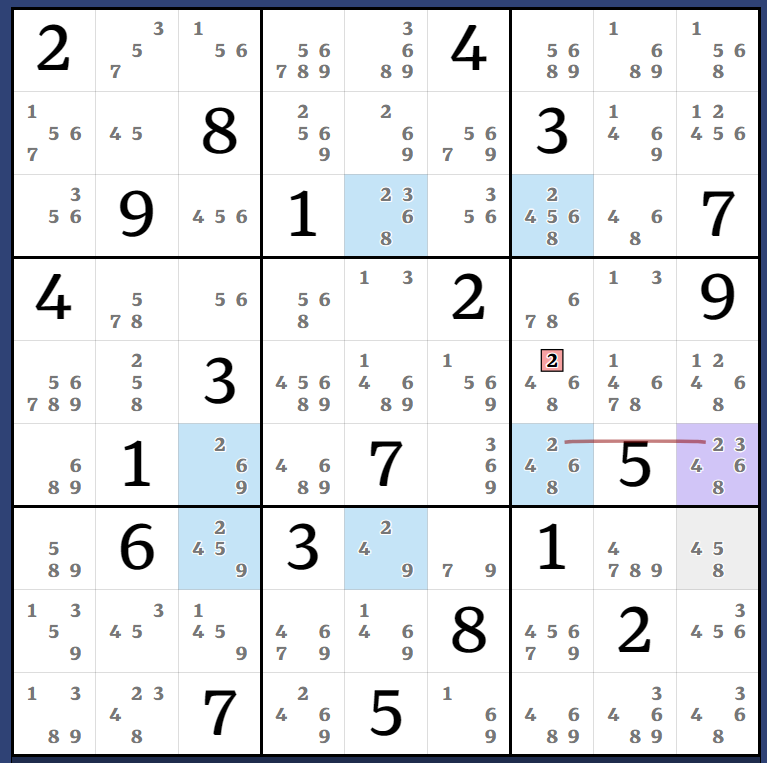
Kraken Row: [(9=7)r7c6 - r7c8 = (7-1)r5c8 = (1-2)r5c9 = r5c2 - r6c3 = (2-9)r7c3 = (9)r7c56] = (1)r5c6 - r4c5 = (1)r8c5 => r8c5<>9
(7)r8c4 = r1c4 - (7=3)r1c2 - (3=54)r28c2 - (4)r9c2 = [(146=2)b8p579 - r9c2 = (2-4)r7c3 = r8c23 - (4=16)b8p59] => r8c4<>46
Kraken Box -> Gross disgusting reduced overlapping ALS AIC. These aren't obscure Sudoku terms I just don't like it because this could be 2 different (non-overlapping) AIC for each of the eliminations, 90% of the length of the chains are identical so there's no point really. To get the 4 elimination you have to consider a sub-chain before the - (4=16)b8p59 link.
Kraken Row: (1)r5c6 = [(9)r7c6 = (9-2)r7c3 = r6c3 - r5c2 = (2-1)r5c9 = (1-7)r5c8 = r7c8 - (7=9)r7c6] => r5c6<>9
Almost ALS-W-Wing: (9)r7c6 = (9-2)r7c3 = (2-4)r9c2 = [(9=5784)r7c1689 - r9c789 = r9c4 - (4=123689)r123478c5] => r2c6<>9
Kraken Row + Kraken Cell: (6)r4c4 = [(1)r5c6 = (1-3)r4c5 = r1c5 - (3=7)r1c2 - r4c2 = (7-6)r4c7 = (6-5)r4c3 = r3c3 - (5=3)r3c6 - r1c5 = (3-1)r4c5 = (1)r5c6] = (6)r3c6 => r5c6<>6
After this move the first digit of the entire solve is placed. Jesus Christ this was like pulling teeth. I can see why they call it unsolvable.
Yes this took way longer than I expected. Not sure if I can keep these up every week, we'll see how long my motivation lasts. Still not sure how valid these AIC DoF extensions I've been trying out are, you could make an argument that they're still using forcing logic, but the chains have no memory and their graphs are still made of alternating strong links & weak inferences which will always lead you to a shared conclusion (the elimination). One thing is for sure, these constructs are very powerful, and classical two-ended AIC will never be able to solve a puzzle this difficult :D
Grouped AIC: (7)r7c8 = (7-5)r8c7 = (5-9)r1c7 = (9)r89c7 => r7c8<>9
Grouped AIC: (9=7)r7c6 - r7c8 = (7-9)r8c7 = (9)r9c78 => r9c46<>9
At this point classical AIC fail us so we need to use branched chains. Read this article if you're unfamiliar with the concept.
You'll see within the square brackets are two "Almost AIC" that are valid save for a single strong link containing 3 candidates rather than 2 - the neat part is that both these extra candidates are in the same cell, so they cannot both be true, therefore both the AIC cannot be false. I'd like to call it something like "Almost X-Chain tie Almost AIC" but it doesn't really need a name.
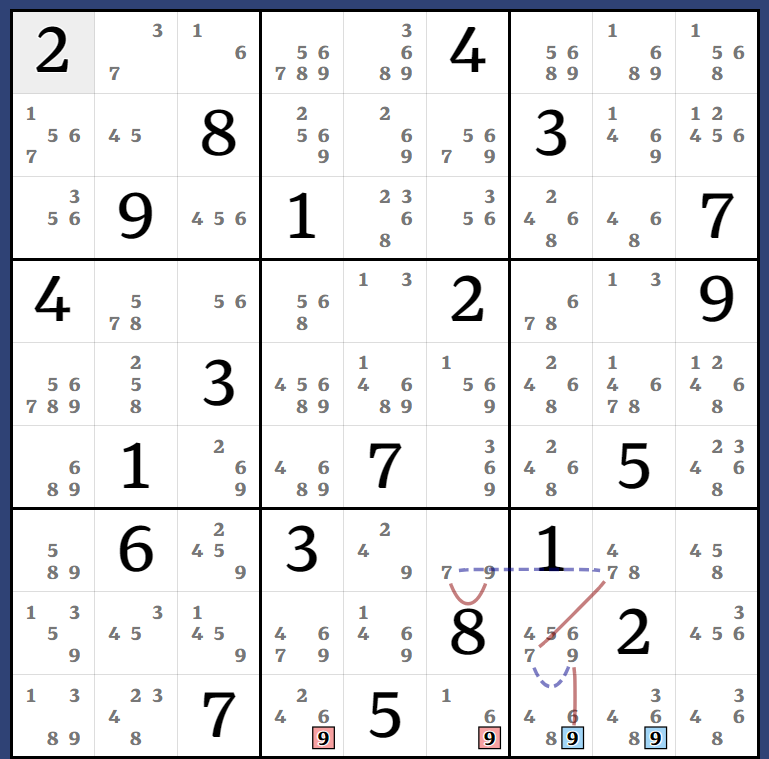
Here's a graph diagram of the chain.
Of course you may have noticed two of the branches converge on the same nodes and share an ending, here's a revised diagram showing that.
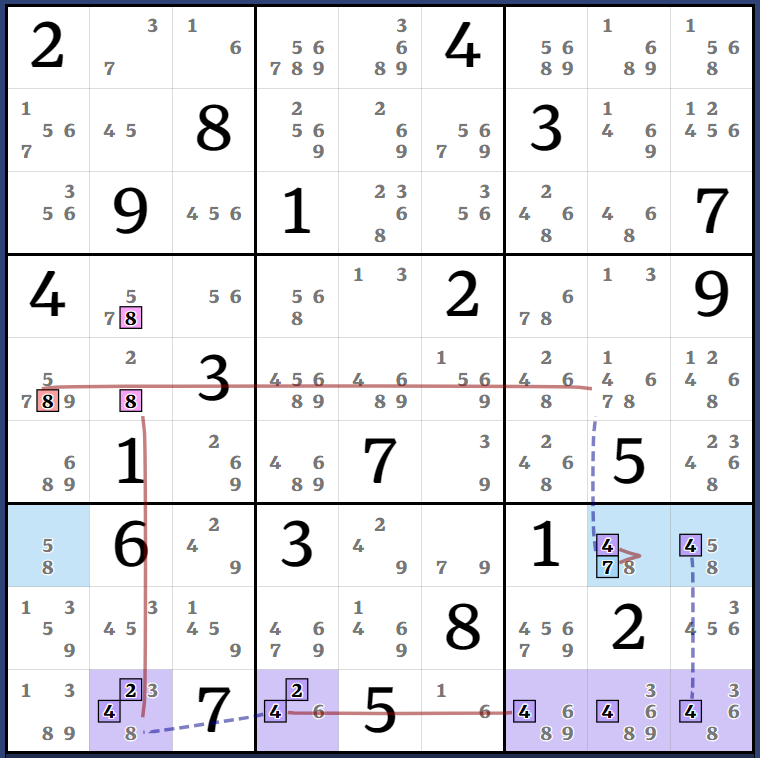
[(1=3)r4c5 - r1c5 = (3-7)r1c2 = (7-1)r2c1 = r9c1 - r9c6 = (1)r5c6] = (1-3)r8c1 = [(1=3)r4c5 - r4c8 = r9c8 - r8c9 = r8c2 - r1c2 = r1c5 - (3=1)r4c5] => r5c5<>1
This is a minor variant of the previous chain. What the previous chain effectively did is prove a strong link between (3)r6c6 and (6)r9c6. With that in mind you can think of this 2nd chain as (1=3)r4c5 - (3)r6c6 = (6-1)r9c6 = (1)r5c6.
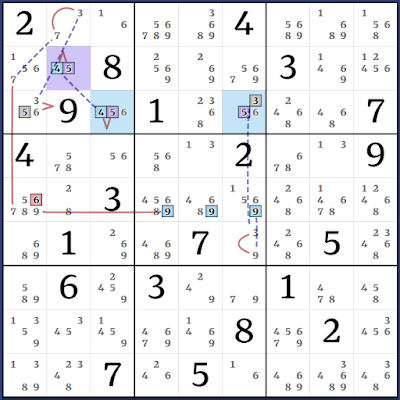
Again we have two Almost-AIC joined by two strong links. This time one of them is an XY-Wing. The extra candidates are joined by the weak link 5r3 so both AIC cannot be false at once. All ends see 5r5c2.
This is an Almost-AIC with an Almost-XYZ-Wing transport to eventually loop back to r5c1 and provide the elimination. There's a Kraken cell in r3c1 and an AALS in r3c36. Definitely need an MSPaint graph to grasp this one.
[(2)r7c3 = (2-9)r6c3 = r78c3 - (9=458)r7c189] = (7)r7c8 - r5c8 = (7-5)r5c1 = [(5)r4c3 = r4c2 - (5=4)r2c2 - (4=56)r34c3]
Two connected Almost-AIC again. Don't think this one requires an explanation
[(9)r5c1 = r5c456 - (9=3)r6c6 - r3c6 = (3-28)r3c5 = (28)r3c78) - (8)r7c8 = (58)r7c19] = (3)r3c1 - (3=7)r1c2 - r2c1 = r2c6 - (7=9)r7c6 => r7c1<>9
A cute Almost-AHS-AIC with a couple added strong links to loop the errant 3 back around to the 9r7c1 elimination.
Grouped ALS-AHS-AIC: (7)r5c1 = r5c8 - (7=584)r7c189 - (4)r9c789 = (24)r9c24 - (8)r9c2 = r45c2 => r5c1<>8
What a relief it is to see a normal AIC after all this.
Still fairly vanilla compared to earlier.
(7)r8c4 = r1c4 - (7=3)r1c2 - (3=54)r28c2 - (4)r9c2 = [(146=2)b8p579 - r9c2 = (2-4)r7c3 = r8c23 - (4=16)b8p59] => r8c4<>46
Kraken Box -> Gross disgusting reduced overlapping ALS AIC. These aren't obscure Sudoku terms I just don't like it because this could be 2 different (non-overlapping) AIC for each of the eliminations, 90% of the length of the chains are identical so there's no point really. To get the 4 elimination you have to consider a sub-chain before the - (4=16)b8p59 link.
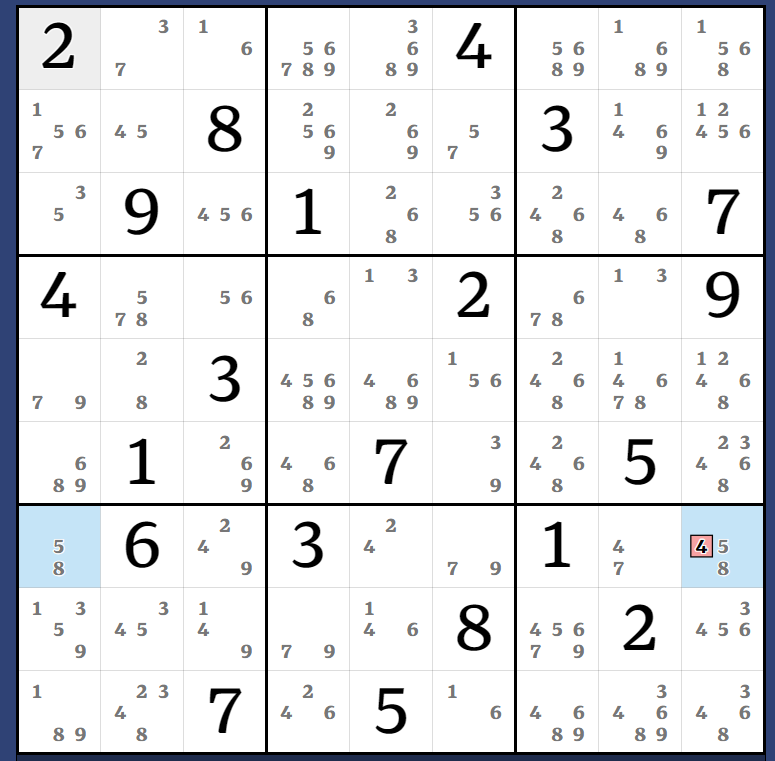
Naked Pair
Grouped AIC: (9)r8c4 = (9-7)r7c6 = r7c8 - r5c8 = (7-9)r5c1 = (9)r5c456 => r6c4<>9
If you remember our virtual strong link from earlier you can express this as (6)r9c6 = (3)r4c5 = (3-9)r6c6 = (79)r27c6. Cute but no point any more :D
Almost ALS-W-Wing: (9)r7c6 = (9-2)r7c3 = (2-4)r9c2 = [(9=5784)r7c1689 - r9c789 = r9c4 - (4=123689)r123478c5] => r2c6<>9
Alternatively you can use (4)r78c5 = (4-9)r5c5 = (9)r12c5 instead of the purple ALS but I didn't realise this until later.
ALC
Finned Swordfish
Grouped AIC-Ring: (7)r5c1 = r5c8 - r7c8 = (7-9)r7c6 = r6c6 - r5c45 = (9)r5c1- => r5c1<>5
ALS-AIC: (5)r4c3 = r4c2 - (5=4)r2c2 - (4=65)r34c3 => r8c3<>5
AHS-AIC: (3)r3c1 = (3-7)r1c2 = r2c1 - r5c1 = (7-5)r4c2 = r4c3 - (5)r3c3 = (35)r3c16 => r3c1<>6
Hidden Pair
AHS-AIC: (8=6)r4c4 - (6=5)r5c4 - (5)r3c3 = (35)r3c16 - (6)r3c6 = (16)r59c6 - (5)r5c6 = (5)r5c4 => r5c4<>8
Kraken Row + Kraken Cell: (6)r4c4 = [(1)r5c6 = (1-3)r4c5 = r1c5 - (3=7)r1c2 - r4c2 = (7-6)r4c7 = (6-5)r4c3 = r3c3 - (5=3)r3c6 - r1c5 = (3-1)r4c5 = (1)r5c6] = (6)r3c6 => r5c6<>6
Bit of a weird one because the Almost-AIC loops back on itself. This is because I had to set it up as a transport to squeeze an elimination out of it. Thankfully this means the extra candidates in the Kraken strong links directly see r5c6 so nothing more is needed from them.
By the way, after this move the puzzle has an SE of 7.2 and no longer requires these insane branched chains. I'll speed through the rest. I've been solving this for 11 hours!
AIC: (5=1)r5c6 - (1=3)r4c5 - r1c5 = (3)r3c6 => r3c6<>5
Naked Pair
Naked Triple
XY-Wing
Then a ton of singles :D
AIC: (2)r9c4 = r9c2 - r5c2 = (2-1)r5c9 = (1-5)r2c9 = (5)r2c4 => r2c4<>2
STTE


































Comments
Post a Comment