Sudokuwiki.org's Weekly 'Unsolvable' Sudoku #642

-

In this post I'll be tackling the weekly "Unsolvable" puzzle from SudokuWiki. This week's puzzle was provided by Richard Kröger. 


Puzzle string: .....1....7..3.5..4..6....9..2...3......7..8.9..4.......1..5..2.3....7..5...8..6. - Sudoku.Coach

SE: 9.3

You may notice I did not publish an article for puzzle #641. This is because it was too hard for me and I couldn't solve it! Sorry to disappoint.

Finned Swordfish

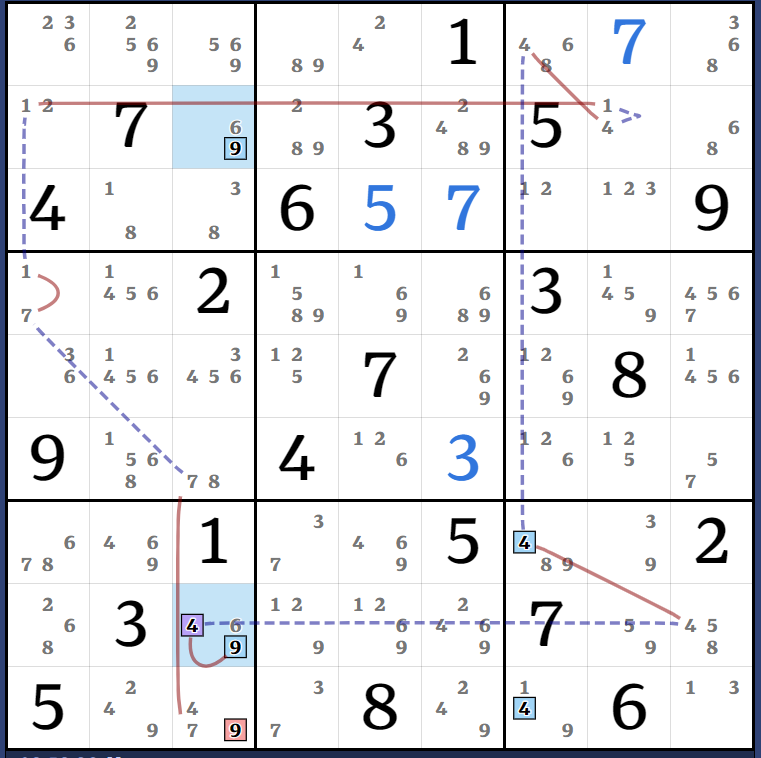
(3)r3c3 = r3c8 - r7c8 = (3-7)r7c4 = r7c1 - r4c1 = (7)r6c3 => r6c3<>3

(7)r6c3 = r9c3 - r7c1 = (7-3)r7c4 = r7c8 - r9c9 = (3-7)r1c9 = (7)r46c9 => r6c8<>7


(2)r3c27 = [(2=5)r3c5 - (5)r3c2 = [(7)r3c6 = r9c6 - r7c4 = (7-8)r7c1 = [(8)r7c2 = r7c7 - r8c9 = r12c9 - (8=1)r3c7 - (1=8)r3c2] - (8)r6c2 = (8-7)r6c3 = r9c3 - r9c6 = (7)r3c6]] => r3c6<>2

Expect to see r3 ALS/AHS used a lot in this article. A large portion of this chain feels redundant but I couldn't reduce it any further. Originally found as a big Kraken X-Wing but it's easier to put into notation this way.

By the same token:


(5)r3c2 = [(5=2)r3c5 - (2)r3c27 = [(3)r3c3 = r3c8 - r1c9 = r9c9 - r9c4 = (3-7)r7c4 = (7-8)r7c1 = [(8)r7c2 = r7c7 - (8=1)r3c7 - (1=8)r3c2] - (8)r6c2 = (8-7)r6c3 = r9c3 - r7c1 = (7-3)r7c4 = r9c4 - r9c9 = r1c9 - r3c8 = (3)r3c3]] => r3c3<>5


(2)r1c5 = [(2)r1c12 = [(2)r5c7 = r6c78 - (2)r6c5 = [(2)r3c5 = r8c5 - r8c1 = (2)r9c2] - (2)r3c2 = (2-1)r1c2 = r3c2 - (1=3782)r3c3678]] => r1c7<>2

Almost ER with an Almost-Transport into an ALS.


(2)r2c4 = [(3)r9c4 = (3-7)r7c4 = [(13)(r9c49=r9c7) - (1)r3c567 = [(7)r9c4 = r1c4 - (7=825)r3c567 - (25)r3c2 = [(2)r9c2 = r1c2 - (59)(b1p2=b1p36) - (9=8)r2c4 - (8=7)r3c6 - r1c4 = (7)r9c4]]]] => r9c4<>2

Nice use of an ALS to tie up 2 Kraken candidates at once. I tried to extend this to eliminate 9r9c4 but it never worked out.


(7)r1c4 = [(7)r6c9 = (7-8)r6c3 = r6c2 - (8)r7c2 = [(7)r6c9 = r6c3 - r4c1 = (7-8)r7c1 = r7c7 - (8)r13c7 = [(68)(b3p36=b3p1) - (4)r1c7 = [(8)r7c1 = (8)r7c7 - (49)(r7c7=r59c7) - (13)(r9c7=r9c49) - (7)r9c4 = (7)r7c4] - (7)r7c1 = r4c1 - r6c3 = (7)r6c9]]] => r1c9<>7


Grouped Kraken AHS: (2=36895)b1p12369 - (5)r3c2 = [(25)(r3c578=r3c2) - (2)r9c2 = (2-7)r9c6 = r3c6 - r1c4 = (7)r1c8] => r1c8<>2


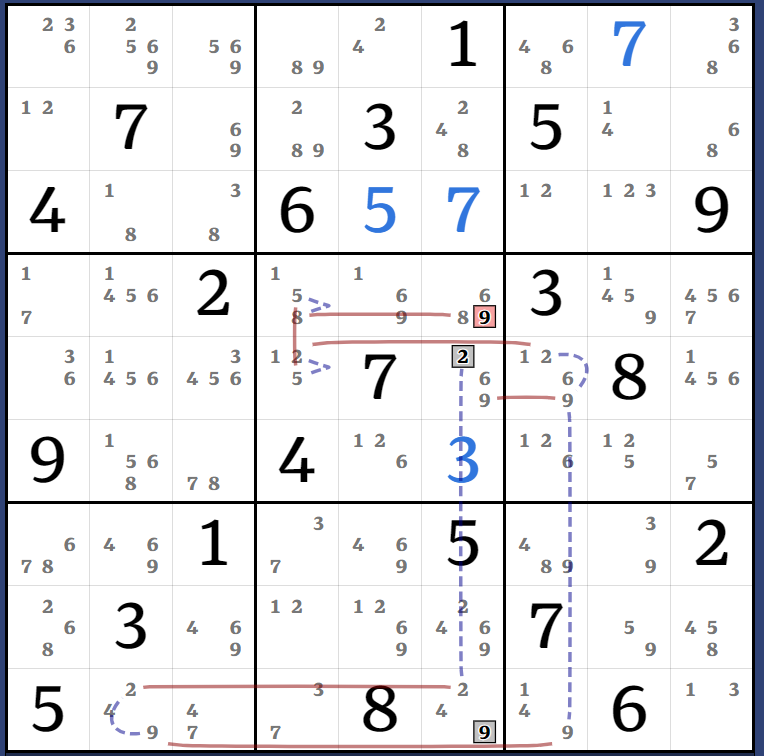
(9)r7c2 = [(9)r2c4 = [(3)r7c4 = r7c8 - r9c9 = (3-7)r9c4 = [(3)r7c4 = r7c8 - (3)r1c8 = [(7)r7c4 = r1c4 - (7=4)r1c8 - r1c5 = (4-9)r2c6 = r2c3 - r1c2 = (9-2)r9c2 = (2-7)r9c6 = (7)r7c4]]] => r7c4<>9

(7)r1c8 = r1c4 - (7=3)r7c4 - (37)(r7c8=r13c8) => r1c8<>4


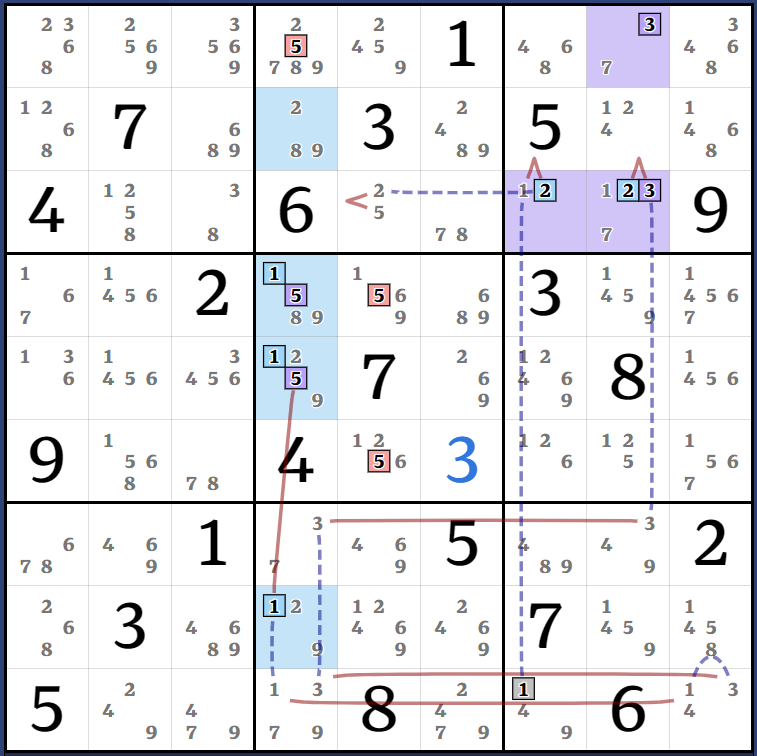
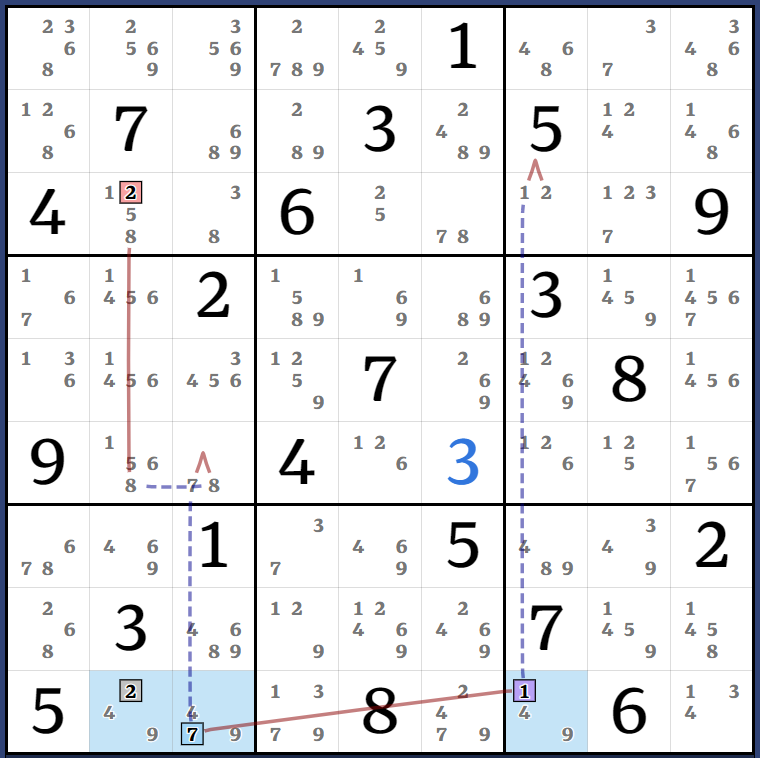
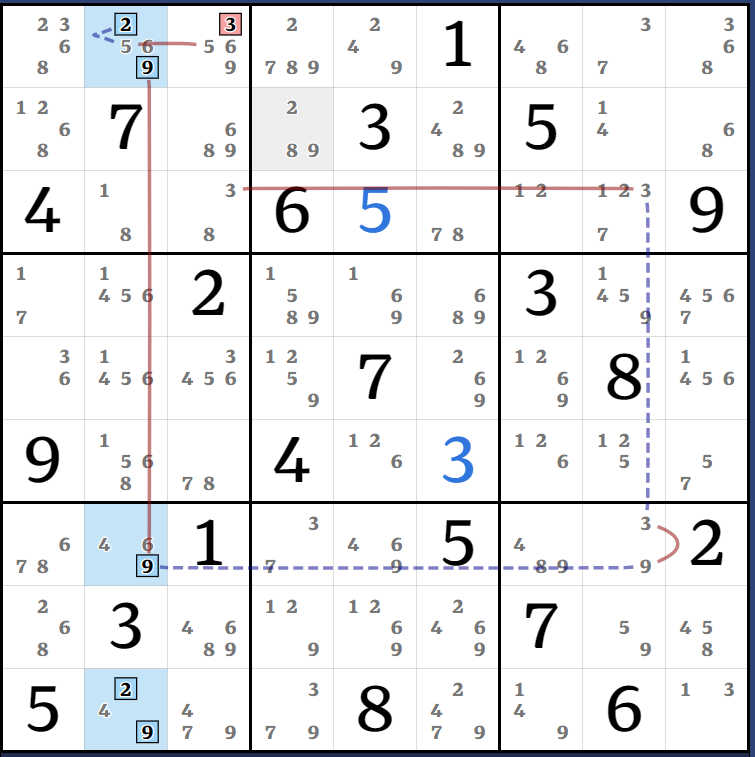
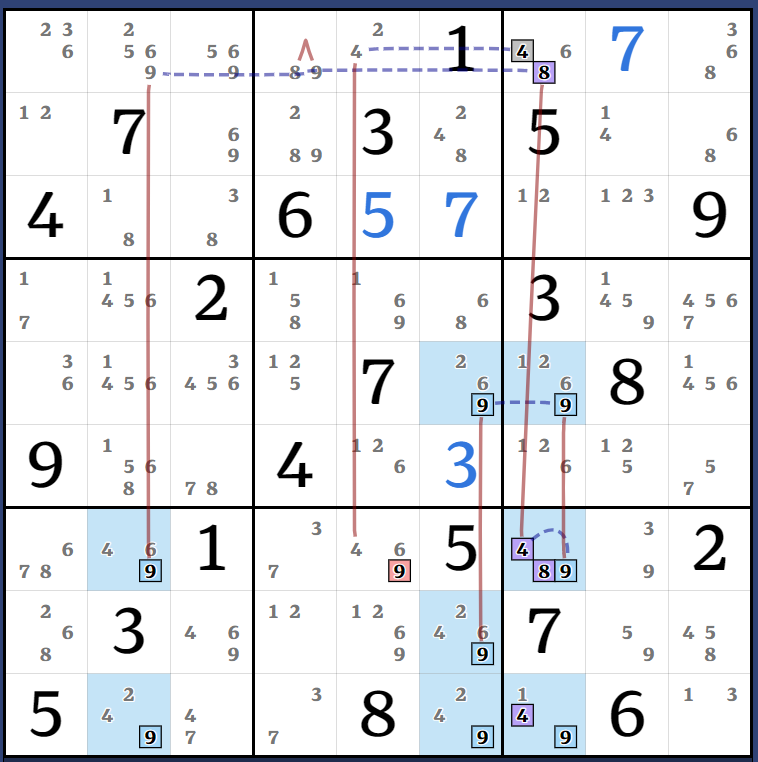
This one had too much overlapping nonsense so I split it into 3 diagrams. It's all based on the AALS (123678)r1278c1. 3 is easy to discount so these diagrams use the ALS (12678)r1278c1. Left diagram is minus the Kraken candidates 8r12c1, middle is for 8r2c1, right is showing the Almost-AIC that is tied to 8r1c1. Unfortunately I couldn't find any simpler way to weakly link 8r1c1 to 8r7c2. 

(8)r6c2 = r6c3 - (8=3)r3c3 - (3)r1c1 = [(8)r6c2 = (8-7)r6c3 = r4c1 - (7=268)r178c1 - (8)r2c1 = [(8)r7c7 = (8-12)r3c7 = [(8)r6c2 = (8-7)r6c3 = r4c1 - (7=2681)r1278c1 - r2c9 = (12)r23c8 - (12=5)r6c8 - r8c8 = (5-8)r8c9 = r2c9 - r3c7 = (8)r7c7]]] => r7c2<>8


(1)r3c7 = [(8=3)r3c3 - r5c3 = (3-1)r5c1 = [(8)r7c7 = r7c1 - r8c13 = (8-5)r8c9 = r8c8 - (5)r6c8 = [(8)r7c7 = (8-7)r7c1 = (7-1)r4c1 = r2c1 - r2c9 = r23c8 - (1=2)r6c8 - r56c7 = (2)r3c7]]] => r3c7<>8

(8)r6c2 = (8-7)r6c3 = r9c3 - r9c6 = (7-8)r3c6 = (8)r3c23 => r1c2<>8

AALS-Ring: (8=512)r3c257 - (12=73)r13c8 - r7c8 = (3-7)r7c4 = r7c1 - r9c3 = (7-8)r6c3 = (8)r6c2- => r6c3<>56
Shame this doesn't result in more eliminations.

Kraken Column: (8)r3c23 = r3c6 - r4c6 = (8-5)r4c4 = [(8)r3c23 = (8-7)r3c6 = r3c8 - r1c8 = (7-5)r1c4 = r5c4 - r5c3 = (5)r1c3] => r1c3<>8

Kraken Row: (5=2)r3c5 - (2=1)r3c7 - (1)r9c7 = [(5=2)r3c5 - (2=173)b3p278 - r7c8 = r7c4 - r9c4 = (3-1)r9c9 = r9c4 - (1=2895)r2458c4] => r1c4, r46c5<>5

Kraken AALS: (2)r3c2 = [(2=1)r3c7 - (1=497)r9c237 - (7=8)r6c3 - r6c2 = (8)r3c2] => r3c2<>2


Kraken X-Wing tie ALS AIC: (3)r9c9 = r1c9 - (3=1274)b3p2578 - (4)r2c6 = [(4)c36\r89 = (4)r5c3 - (4)r5c7 = [(4)r79c7 = r1c7 - (4=1273)b3p2578 - r1c9 = (3)r9c9]] => r9c9<>4

(1=3)r9c9 - r9c4 = (3-7)r7c4 = r7c1 - r4c1 = (7)r4c9 => r4c9<>1


(5=2)r3c5 - (2=1)r3c7 - (1)r9c7 = [(5)r1c3 = r5c3 - r5c4 = (5-8)r4c4 = r4c6 - (8)r3c6 = [(5=1273)r3c5678 - r1c9 = (3-1)r9c9 = r9c4 - (37)(b8p7 = b8p19) - (7=8)r3c6 - r4c6 = (8-5)r3c3 = r5c4 - r5c3 = (5)r1c3]] => r1c5, r3c2<>5

This places 5r3c5.

(7)r6c9 = (7-8)r6c3 = r6c2 - (8=12)r3c27 - r3c8 = (2)r6c8 - (578)(r6c8 = r6c239) => r6c9<>16

(4=1)r2c8 - r2c1 = (1-8)r3c2 = r6c2 - (8=7)r6c3 - (7=5)r6c9 - r8c9 = (5)r8c8 => r8c8<>4

(1=3)r9c9 - r9c4 = (3-7)r7c4 = r7c1 - r4c1 = r4c9 - (7=5)r6c9 - r8c9 = (5)r8c8 => r8c8<>1


Kraken AALS: (1=3)r9c9 - (3=4698)r7c2578 - (8)r8c9 = [(1=4576)r4568c9 - (6=21)r36c7 - r9c7 = (1)r89c9] => r2c9<>1

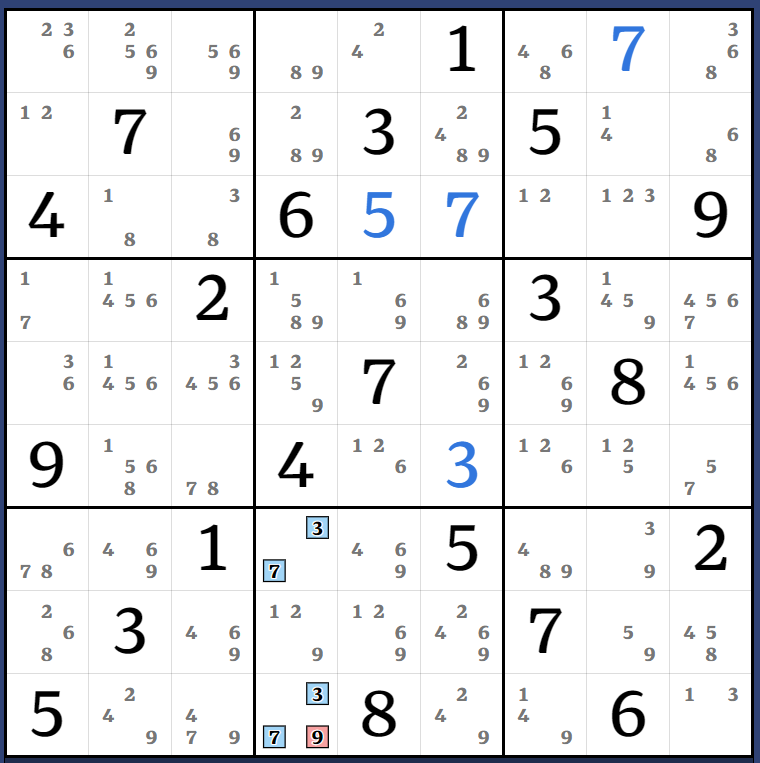
This isn't a hugely complex move but I made the image full sized because I love the colours.


Almost W-Wing Transport: (1)r5c9 = [(3)r5c1 = r1c1 - r1c9 = (3-1)r9c9 = r8c9 - r8c45 = (1-7)r9c4 = [(8=7)r6c3 - r9c3 = r9c6 - (7=8)r3c6] - (8=3)r3c3 - r1c1 = (3)r5c1] => r5c1<>1

This move also gives us the virtual strong link 3r5c1 = 1r5c9, or 3r5c1 = 3r9c9.

Ring: (1=8)r3c2 - r6c2 = (8-7)r6c3 = (7-1)r4c1 = (1)r2c1- => r4c1<>6


(1)r5c9 = [(1)r8c45 = r9c4 - (1)r5c4 = [(8=1)r3c2 - r2c1 = r4c1 - r5c2 = (1-9)r5c7 = r5c46 - (9)r4c56 = [(8=1)r3c2 - r2c1 = r4c1 - (1=68)r4c56]] - (8=7)r3c6 - (37)(r1c4 = r79c4) - (1)r9c4 = (1)r8c45] => r8c9<>1

This should be the last big move of the solve, it is significantly easier now.


Kraken ALS Transport: (4)r8c9 = [(7=58)r68c9 - r7c7 = (8-7)r7c1 = (7)r9c3] - (7)r6c3 = (7-1)r4c1 = r2c1 - (1=4)r2c8 => r12c9, r7c8<>4

ER

Sashimi Swordfish

AHS-AIC: (3)r3c3 = r3c8 - (3=9)r7c8 - (29)(r7c2 = r19c2) - (5)r1c2 = (5)r1c3 => r1c3<>3

Kraken Row: (8)r8c1 = [(8)r3c23 = (8-7)r3c6 = (7-2)r9c6 = r9c2 - (2=6)r8c1 - r8c56 = (6-4)r7c5 = r1c5 - r1c7 = (4-1)r2c8 = (1)r2c1] => r2c1<>8

the same with a little transport: (1)r2c1 - (1=8)r3c2 => r1c1<>8

Kraken Cell: (9)r1c2 = r7c2 - (9)r8c3 = [(4)r1c5 = (4-6)r7c5 = r7c12 - (6=4)r8c3 - r8c9 = r79c7 - r1c7 = (4)r1c5] => r1c5<>9

Ring: (2=4)r1c5 - r1c7 = (4-1)r2c8 = (1-2)r2c1 = (2)r2c46- => r1c4<>2, r2c1<>6

ALS-XZ: (8=12)b1p48 - (2=3798)r1279c4 => r3c6<>8

Hidden Pair

Kraken Cell: (9=8)r1c4 - (8)r1c7 = [(9=284)b2p124 - (4=6)r1c7 - (6=129)r356c7] => r5c4<>9

(9=64)r28c3 - r8c9 = r79c7 - r1c7 = (4-1)r2c8 = r2c1 - (1=7)r4c1 - r6c3 = (7)r9c3 => r9c3<>9

Kraken X-Wing: (9)r59\c67 = (9-2)r9c2 = (2)r1c2 - (59)(r1c2 = r1c34) => r2c6<>9

(9)r9c6 = [(9)r5c6 = r5c7 - r9c7 = (9-2)r9c2 = r9c6 - (2)r5c6 = [(8)r4c6 = (8-5)r4c4 = (5-2)r5c4 = (2-9)r5c7 = (9)r5c6]] => r4c6<>9

Kraken Finned Swordfish: (4)r7c5 = r1c5 - (4)r1c7 = [(9)c267\r579b8 = r1c2 - (9=8)r1c4 - (48)(r1c7 = r79c7) - (9)r79c7 = r5c7 - r5c6 = (9)r89c6] => r7c5<>9

(6=4)r7c5 - (4=2)r1c5 - (2=36)r15c1 => r7c1<>6

(9=378)r7c148 - r8c1 = (8-5)r8c9 = (5)r8c8 => r8c8<>9

Naked Triple

(6)r6c7 = r6c5 - (6=4)r7c5 - r1c5 = (4)r1c7 => r1c7<>6

(6=4)r7c5 - r89c6 = r2c6 - r2c8 = (4-9)r4c8 = (9)r4c5 => r4c5<>6

(6=4)r7c5 - r1c5 = (4-8)r2c6 = (8-6)r4c6 = (6)r4c2 => r7c2<>6

STTE

Definitely easier than #640, probably also easier than #639. Or perhaps I've gotten used to solving these horrid puzzles. This was an effort over 3 days, Sudoku.Coach says I took 4h07m but that doesn't include my time fiddling around in Xsudo. Puzzle #643 will be posted tomorrow, let's hope it's not another SE 9.4 monstrosity...





















Comments

Post a Comment

Popular posts from this blog

Impossible pattern chaining in an SE 9.0 challenge from Reddit

-
Image
Here's a puzzle generated by Sudoku.Coach and posted by u/ddalbabo on Reddit. SC's "Beyond Hell" grids are always a treat, often on the very edge of requiring Forcing Chains. Discussion link Puzzle string: 010000800025060000780001904000300000050100009800000010000020540090800106003600000 Sudoku.Coach SE = 9.0 according to SukakuExplainer. YZF says 8.8. Not sure what's going on there After basics (7)r6c49 = (4)r6c4 - (4=9)r2c4 - r2c1 = r4c1 - r6c3 = (9)r6c5 => r6c5<>7 What immediately jumps out to me is this Bivalue Oddagon of {25}. We can build an AIC off the guardians and eliminate a 7. I couldn't find any other more useful chains using this so it's back to the drawing board for now. The next move uses a DoF>1 AIC so read  this article  if you haven't already. (4)r6c7 = [(4)r8c5 = r9c6 - r9c2 = r4c2 - (4=26)r46c7 - (2=7)r9c7 - (7=4)r9c2 - r9c6 = (4)r8c5] => r6c5<>4 You could call this a Kraken ALS? The 2 DoF component here is (4)r4...
Read more

Sudokuwiki.org's Weekly 'Unsolvable' Sudoku #640

-
Image
 In this post I'll be tackling the weekly "Unsolvable" puzzle from  SudokuWiki . This week's puzzle was provided by Richard Kröger, as with last week's.  Puzzle string: .....8.7.....5...9...2.43...8..4..6.5....3.....27....19....6..5..7.1..8..3....4.. Sudoku.Coach SE: 9.2 It turns out 9.2 is way  harder than 9.0, so buckle up, we're going to be here for a while. No basics to start off with, it's straight into the fire. [(9=5)r6c6 - (5=9)r8c6 - r8c7 = (9)r456c7] = (2)r8c6 - (2)r4c6 = [(9=5)r6c6 - r4c46 = (5-2)r4c7 = (2-3)r4c9 = (3)r6c8] => r6c8<>9 If you're unfamiliar with my use of almost-AICs you may want to read  this post  before proceeding. This elimination comes from two chains that "almost" eliminate 9r6c8, save for one of the strong links in each having 3 nodes rather than 2 - but these extraneous nodes are actually both contained within the same column, so they cannot both be true at once, hence the AICs cannot both be false a...
Read more

Solving "Impossible #1" with DoF>1 AIC

-
Image
I've been learning advanced Sudoku tactics for about 2 years now and lately I've been venturing into the world of branched AIC. It's very work-intensive to identify useful examples, but the results are equally rewarding. In this post I'll be solving the puzzle "Impossible #1" by the Sudoku.Coach user "Public github database". I don't know what their username is about, I couldn't find this puzzle on Github or anywhere else, and they have yet to post another puzzle - but it was an interesting solve nonetheless.  You may play the puzzle here:  https://sudoku.coach/en/s/6gcT Of course there are spoilers below, so now's the time to try it yourself if you're interested in doing so. Required knowledge for this article: AIC, Rings, ALS, ALC, UR, the ability to research terms you don't understand. There are a lot of images so I kept them small, click to enlarge if you want to see the details. Quick overview of the difficulty Puzzle string:...
Read more