SE 9.0 from Reddit 2025-05-15
u/Ok_Application5897 posted this puzzle on the Reddit today:
......789..87.42.3.......4....6.3891..15..3.2......4..1349..528.2548193.8.9235..4 - Sudoku.Coach
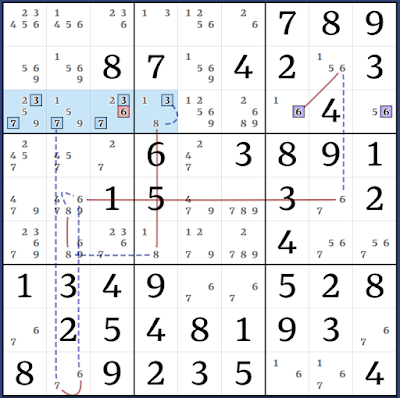
AAHS-AIC: (6=2)r1c6 - (2)r6c6 = [(6)r1c3 = r6c3 - (23)(r6c3 = r6c15) - (1)r6c5 = r123c5 - (1=3)r1c4 - (3=26)r1c36] => r125c6<>6
Kraken Cell: (6)r6c3 = r1c3 - (6)r2c1 = [(5)r6c8 = r2c8 - (5=9)r2c1 - (89)(r23c2 = r56c2) - (6)r56c2 = (6)r6c13] => r6c8<>6
Kraken Cell+Column: (6)r6c9 = [(6)r9c2 = r8c1 - (6)r2c1 = [(6)r9c2 = r8c1 - r8c9 = (6-5)r3c9 = r2c8 - (5=9)r2c1 - (89)(r23c2 = r56c2)]] => r6c2<>6
Kraken Row: (36)(r6c1 = r6c39) - (7)r6c9 = r8c9 - r9c8 = r9c2 - (7)r3c2 = [(2=7)r4c3 - r3c3 = (7-3)r3c1 = r13c3 - r6c3 = (3)r6c1] => r6c1<>2
Kraken Cell+Row: (7=2)r4c3 - (2)r1|3c3 = [(2)r3c1 = r3c56 - (2=6)r1c6 - (6=3)r1c3] - (3)r3c1 = (3)r6c1 => r6c1<>7
Almost-Almost-Sue de Coq: (6)r6c3 = r1c3 - (6)r2c1 = [(6)r6c3 = r1c3 - (6=2)r1c6 - (2)r1c1 = [(2=4597)r1245c1 - (7=2)r4c3-] - (3)r6c3 = (3)r6c1 => r6c3<>27, r6c1<>9
Kraken Cell: (5=96)r2c12 - (6)r1c3 = [(5=7)r6c8 - r6c9 = r8c9 - r8c1 = r45c1 - (7=2)r4c3 - (2=3)r1c3 - (3=1)r1c4 - r2c5 = (1)r2c8] => r2c8<>5
......789..87.42.3.......4....6.3891..15..3.2......4..1349..528.2548193.8.9235..4 - Sudoku.Coach
SE 9.0
Let's get straight into it.
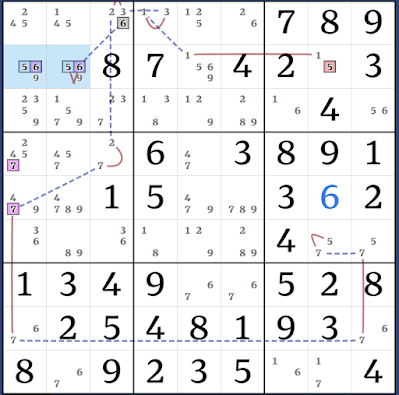
AAHS-AIC: (37)r3c13 = [(6=7)r9c2 - (37)(r3c2 = r3c4) - (8)r4c3 = r6c4 - r6c2 = (8)r5c2] - (6)r5c2 = r5c8 - r2c8 = (6)r3c79 => r3c3<>6
AAHS-AIC: (6=2)r1c6 - (2)r6c6 = [(6)r1c3 = r6c3 - (23)(r6c3 = r6c15) - (1)r6c5 = r123c5 - (1=3)r1c4 - (3=26)r1c36] => r125c6<>6
Kraken Cell: (6)r6c3 = r1c3 - (6)r2c1 = [(5)r6c8 = r2c8 - (5=9)r2c1 - (89)(r23c2 = r56c2) - (6)r56c2 = (6)r6c13] => r6c8<>6
Kraken Cell+Column: (6)r6c9 = [(6)r9c2 = r8c1 - (6)r2c1 = [(6)r9c2 = r8c1 - r8c9 = (6-5)r3c9 = r2c8 - (5=9)r2c1 - (89)(r23c2 = r56c2)]] => r6c2<>6
Kraken AALS: (3=276)r134c3 - (6=2)r1c6 - (2)r6c6 = [(8=97)r6c26 - r6c89 = (7-6)r5c8 = (6-8)r5c2 = (8)r5c6] - r6c4 = (8-3)r3c4 = (3)r1c4 => r1c1<>3
Kraken Row: (36)(r6c1 = r6c39) - (7)r6c9 = r8c9 - r9c8 = r9c2 - (7)r3c2 = [(2=7)r4c3 - r3c3 = (7-3)r3c1 = r13c3 - r6c3 = (3)r6c1] => r6c1<>2
Kraken Cell+Row: (7=2)r4c3 - (2)r1|3c3 = [(2)r3c1 = r3c56 - (2=6)r1c6 - (6=3)r1c3] - (3)r3c1 = (3)r6c1 => r6c1<>7
Almost-Almost-Sue de Coq: (6)r6c3 = r1c3 - (6)r2c1 = [(6)r6c3 = r1c3 - (6=2)r1c6 - (2)r1c1 = [(2=4597)r1245c1 - (7=2)r4c3-] - (3)r6c3 = (3)r6c1 => r6c3<>27, r6c1<>9
This would be an ALS-XZ Ring (or Sue de Coq) if not for the Kraken candidates, but both trivially lead to (6)r6c3, so we can eliminate all joint eliminations. Also I was cheeky and extended this a bit with (6-3)r6c3 = (3)r6c1 to take out a 9, since it's another potential SdC elimination.
Pair
Kraken Row: (5)r3c1 = [(7)r3c3 = (7-2)r4c3 = (2-5)r4c1 = r4c2 - r3c2 = (5-6)r3c9 = r8c9 - (6=7)r8c1] => r3c1<>7
Kraken Cell: (5=96)r2c12 - (6)r1c3 = [(5=7)r6c8 - r6c9 = r8c9 - r8c1 = r45c1 - (7=2)r4c3 - (2=3)r1c3 - (3=1)r1c4 - r2c5 = (1)r2c8] => r2c8<>5
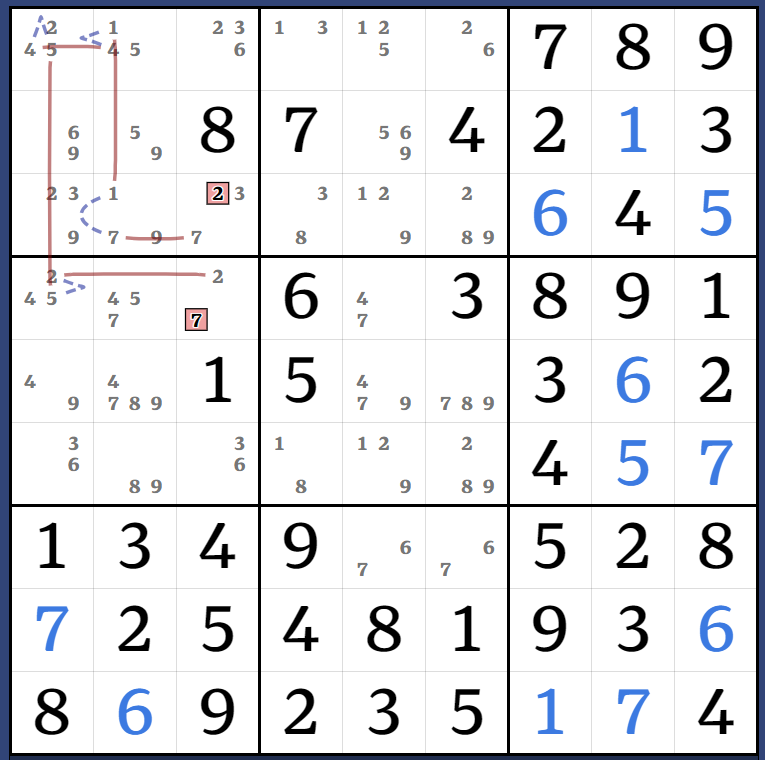
(1)r3c2 = (1-4)r2c1 = r1c1 - (4=9)r5c1 - (9=8)r6c2 - r6c4 = (8)r3c4 => r3c4<>1






















Comments
Post a Comment