Sudokuwiki.org's Weekly 'Unsolvable' Sudoku #646
In this post I'll be tackling the weekly "Unsolvable" puzzle from SudokuWiki. This week's puzzle was provided by Andrew Stuart.
Puzzle String: .5.....82...6......21..73...9.4....8.78....3.1....9.5...29..84......5...93.....7. - Sudoku.Coach
SE: 9.0
Another Andrew Stuart puzzle so I'm hoping it will be on the easier side like the last one.
After basics:
Finned Swordfish
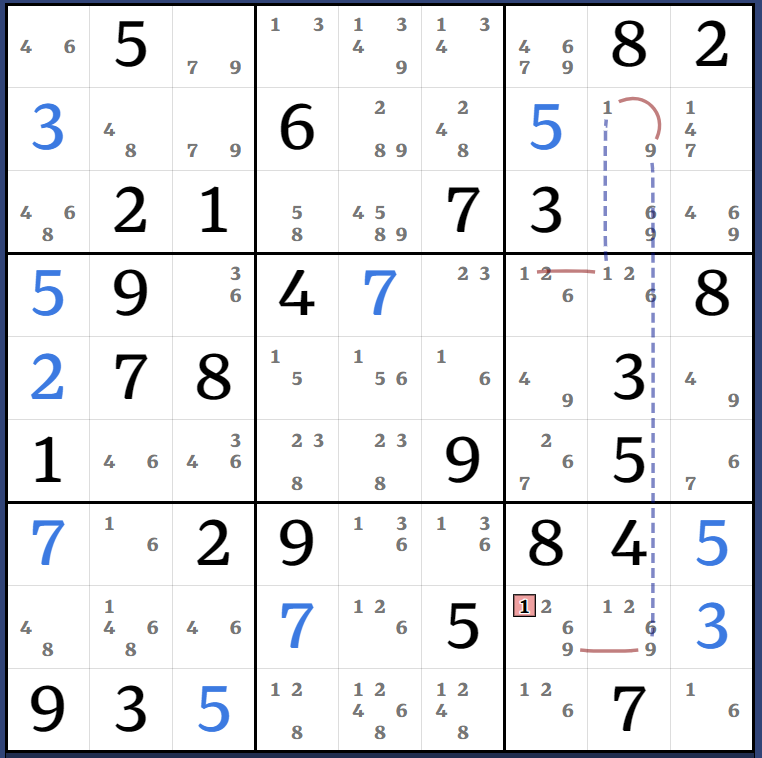
(1=349)r1c456 - r1c3 = r2c3 - (9=1)r2c8 => r1c7, r2c56<>1
(2)r9c456 = r9c7 - (28)(r6c7 = r6c45) - (7)r6c4 = (7)r8c4 => r8c4<>2
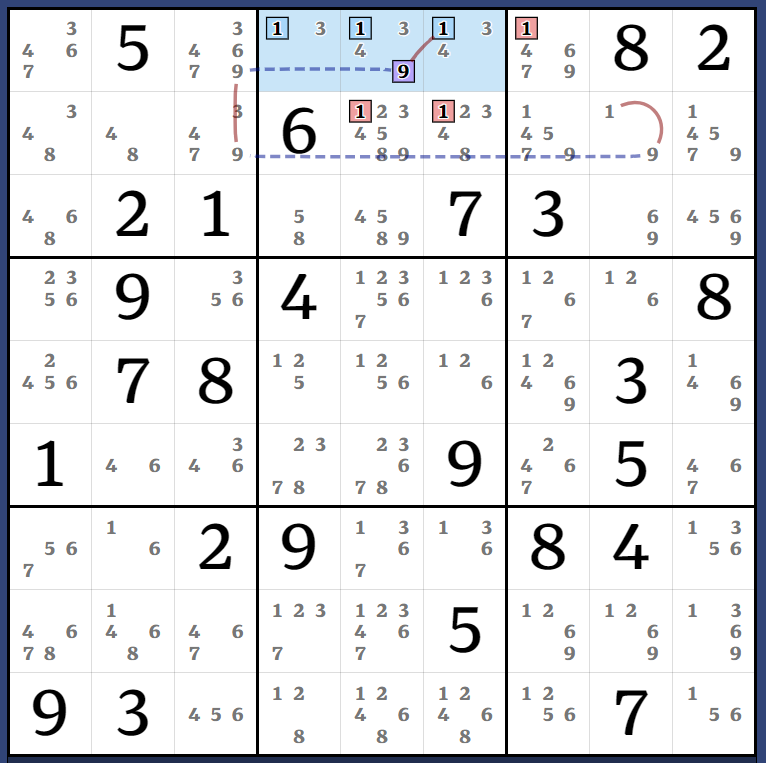
(4=8)r2c2 - r2c6 = (8-4)r9c6 = (4)r12c6 => r2c5<>4
(4=8)r2c2 - r2c6 = (8-4)r9c6 = (4)r12c6 => r2c5<>4
Almost-ALC tie Almost Kraken X-Wing: [(4=8)r2c2 - r23c1 = (8-4)r8c1 = r123c1-] = (4)r5c1 - (4)r5c7 = [(4)c67\r12 = (4-8)r9c6 = r2c6 - (8=4)r2c2] => r12c3<>4
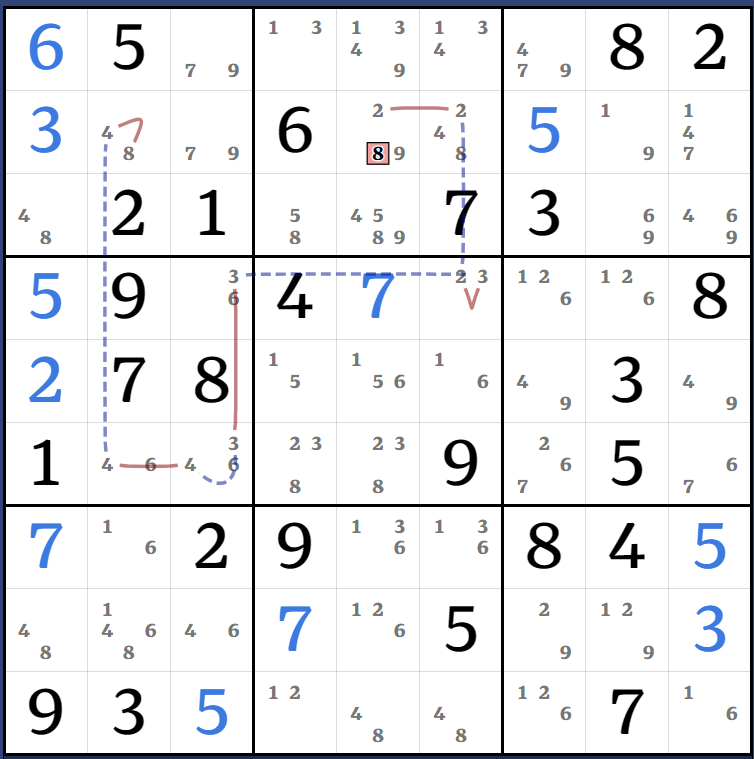
Fairly sure I've run out of easier steps now. Wasn't sure I could get any eliminations off this almost-ALC but found a way to make it work using this double-Kraken X-Wing.
Kraken AHS AIC: (7)r4c5 = r4c7 - r6c9 = (7-1)r2c9 = r2c8 - (1)r4c8 = [(17)(r4c5 = r4c67) - (1=256)r5c456] => r4c5<>256
(8)r6c5 = (8-7)r6c4 = r8c4 - r7c5 = (7-5)r7c1 = r9c3 - r4c3 = (5-2)r4c1 = r5c1 - (2=156)r5c456 => r6c5<>6
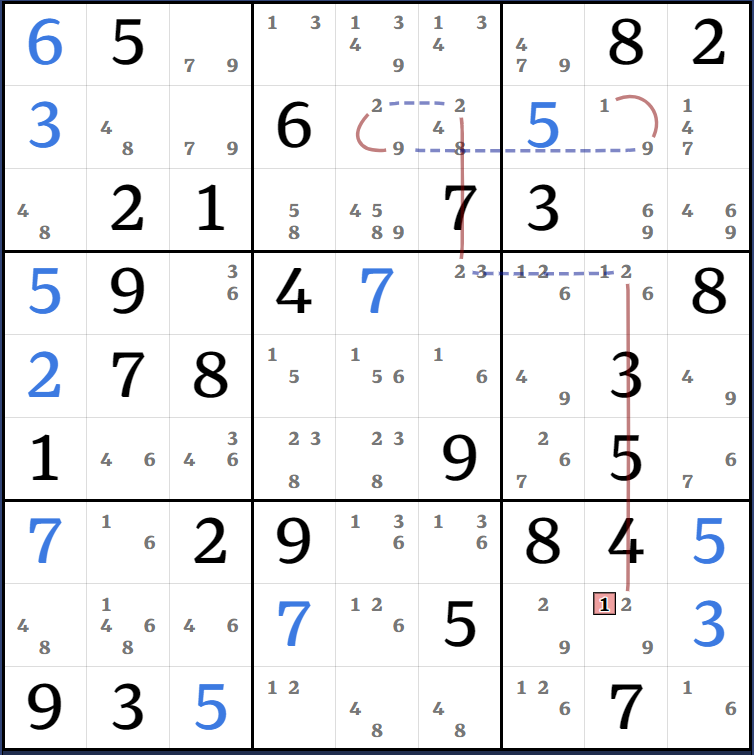
Kraken Cell: (6)r13c1 = r1c3 - (6)r4c3 = [(5)r7c1 = r4c1 - (5=3)r4c3 - (3=467)r6c239 - r6c4 = r46c5 - r7c5 = (7)r7c1] => r7c1<>6
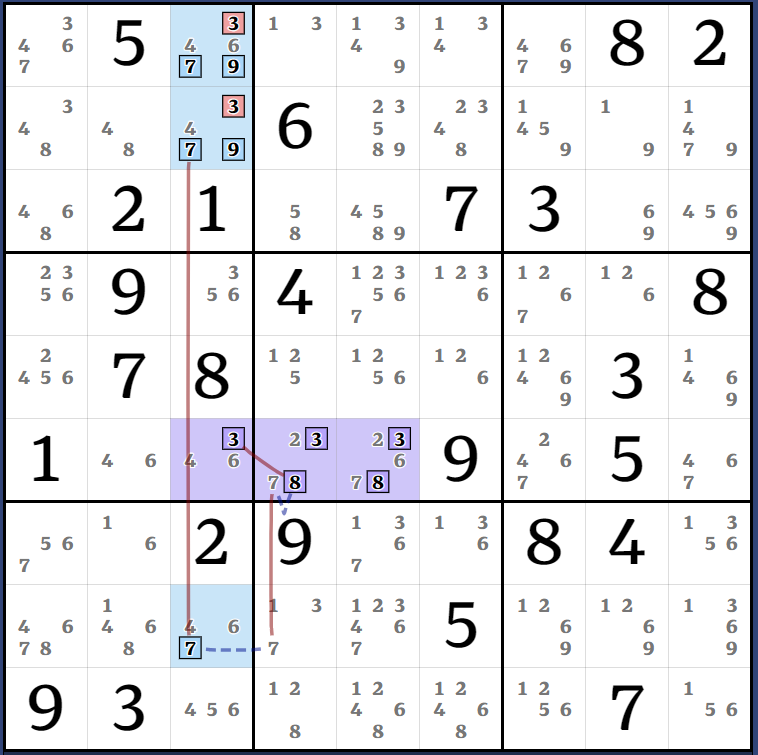
Kraken Cell: (6)r4c8 = [(2)r5c1 = r4c1 - (2=1)r4c8 - (1=9)r2c8 - r2c3 = (9-6)r1c3 = (6)r13c1] - (6)r5c1 = (6)r5c56 => r4c6<>6
Kraken Row: (4)r3c1 = [(4)r5c7 = r12c7 - r3c9 = r3c5 - r12c6 = (4-8)r9c6 = r2c6 - (8=5)r3c4 - (5=194)r5c479] => r5c1<>4
Triple
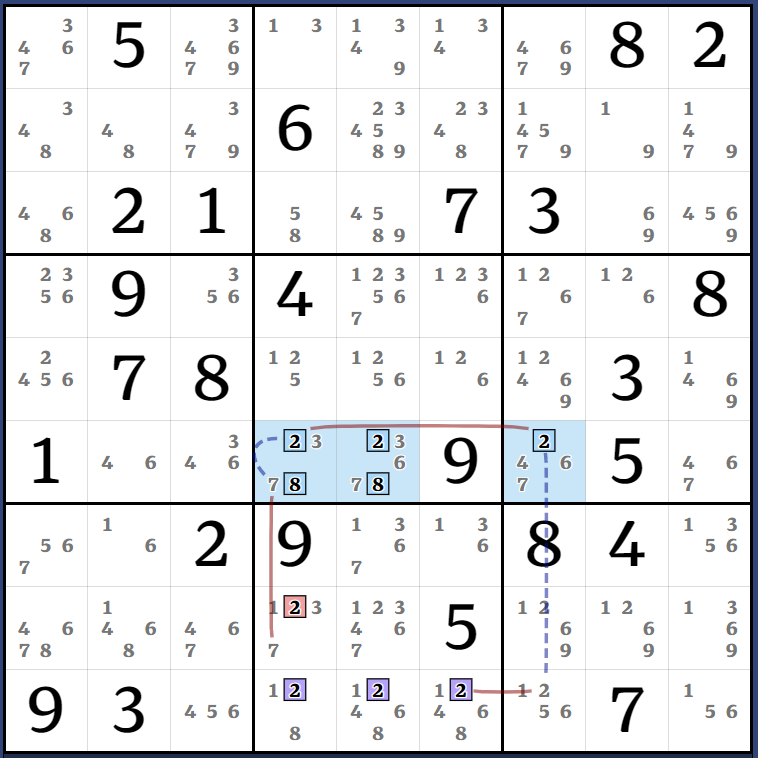
(2)r9c4 = r6c4 - (2=3)r4c6 - r4c3 = (3-4)r6c3 = r6c2 - (4=8)r2c2 - r2c6 = (8)r9c6 => r9c4<>8, r9c6<>2
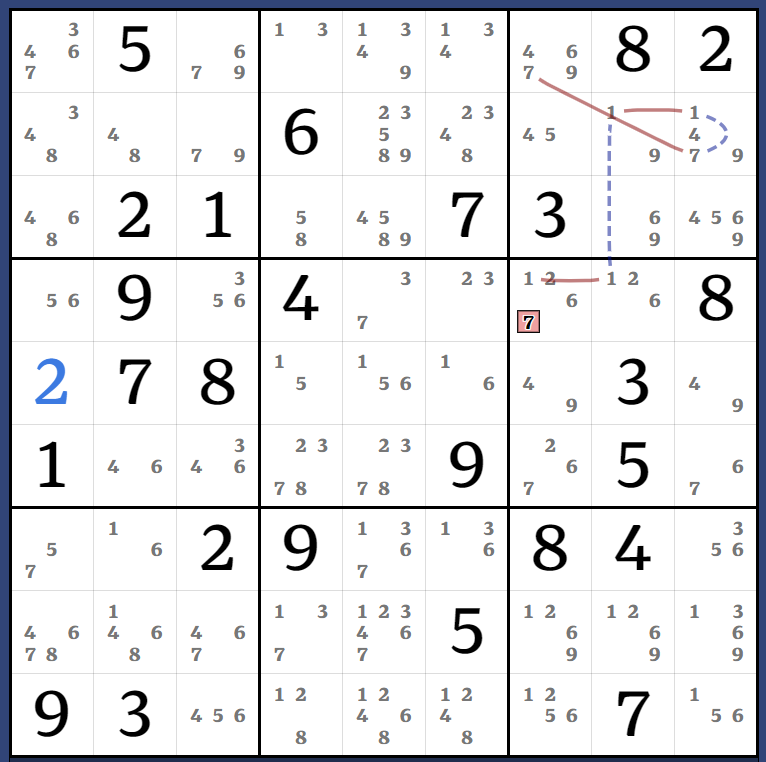
STTE
Again not as difficult as the Kröger puzzles, this one only took me a few hours. That's how long some single steps took in the 9.4 a few weeks ago lol. Some satisfying moves in this week's solve, I think the almost-ALC was the best, but that reminds me I forgot to use the actual ALC when it became available. Whoops!































Comments
Post a Comment